ترجمههای کامران بزرگزاد

خلاصهای از بخشهای کتاب
مباحثی درباره بینهایتِ ریاضی، فرضیه پیوستار، عرفان کابالا، و زندگی گئورگ کانتور
«میبینم، ولی نمیتوانم آن را باور کنم»
لایب نیتس، نسبیت، و قانون اساسی آمریکا
اثبات کوهن و آینده نظریه مجموعهها
توجه: به دلیل کامل نبودن این فایل، ممکن است برخی از لینکهای کار نکنند.
این کتاب درباره مفهوم بینهایتِ ریاضی، فرضیه پیوستار، زندگی گئورگ کانتور، و عرفان کابالا است. این دومین کتابی است که مترجم درباره موضوع بینهایت ترجمه میکند. کتاب قبلی مقدمهای بسیار کوتاه درباره بینهایت، نوشته یان استوارت بود. با وجود اینکه هر دو این کتابها توسط ریاضیدانان معروفی نوشته شدهاند، و میان محتوای آنها همپوشانی قابل توجهی وجود دارد، ولی در کتاب حاضر مطالبی وجود دارد که در کتاب استوارت به آنها پرداخته نشده، یا سریع از روی آنها رد شده. این مطالب عمدتاً درباره عرفان کابالا، زندگی کانتور و همچنین گودل است که در گسترشِ مفهومِ بینهایتِ بالفعل و اصول مربوط به آنها پیشگام بودهاند.
تفاوت عمدهای که این کتاب با کتاب قبلی دارد، فراهم آوردن مقدمهای بر عرفان کابالا است که ظاهراً کانتور در توسعه مفاهیم مربوط به بینهایت تحت تاثیر این مکتب بوده. کابالا و مَرکبا ریشه در عرفان یهودی دارند و از قدیمیترین عرفانهای شناخته شده هستند، که قدمت آنها به قرون اول میلادی باز میگردد. با توجه به اینکه نویسنده این کتاب یک ریاضیدان یهودی است، او جزء کسانی بوده که میتوانستند منبع بهتری برای توضیح مطالب مربوط به کابالا فراهم آورند.
کلاً عرفان به معنای شناخت، شهود، و آگاهی باطنی از حقیقتِ وجود است. معمولاً در تمام عرفانها، از جمله عرفانهای ایرانی/اسلامی، این شناخت نه از طریق عقل و استدلال، بلکه از راه تجربه درونی، سیر و سلوک، و اتصال قلبی با حقیقت یا خداوند حاصل میشود.
عرفانهای اسلامی/ایرانی، که به تصوف نیز معروفند، بیشتر بر پایه تزکیه نفس هستند و هدف آنها رسیدن به عشق الهی است. ابزار این گونه عرفانها معمولاً عبارتند از ذکر، سماع، ریاضت، سرودن شعرهای عرفانی، و شریعتِ همراه با طریقت.
عرفان کابالا که بر آموزههای یهودی قرار دارد، بیشتر بر شناخت ذات خدا (که به عین-سوف معروف است)، درک نظم الهی، و نزدیکی به خدا از طریق فهم رازهای آفرینش قرار دارد. ابزارهای رسیدن به اهداف کابالا عبارتند از تفسیر رمزی تورات، عددشناسی (گماتریا)، مراقبههای یهودی، و تفسیر متون رمزآلود، مانند زوهر (Zohar) است. در مقایسه با دیگر مکاتب عرفانی، کابالا رمزآلودتر است، و به دلیل تکیه بر مراقبههای خاص، حصول به اهداف آن نسبتاً سختتر میباشد.
ارتباط کابالا و مفهومِ فلسفی بینهایت معروف است و شاید در هیچ یک از عرفانها به اندازه کابالا بر مفهوم بینهایت تکیه نشده. اینکه میان ایدههای گئورگ کانتور و کابالا چه ارتباطی وجود دارد خیلی روشن نیست. آیا کانتور پیرو کابالا بوده؟ آیا اصلاً کانتور یهودی بوده که پیرو کابالا باشد؟ در این کتاب سعی شده که به این سئوالات پاسخ داده شود.
حتی اگر کانتور مسیحی هم بوده، ولی معلوم شده که تبار او یهودی است، در نتیجه به احتمال زیاد او با متون کابالا آشنا بوده. محکمترین دلیل آن هم بکارگیری نمادهای عبری (مانند الف و تاو) توسط کانتور است، و گرنه مانند خیلی از دانشمندان غربی میتوانست از نمادهای یونانی/لاتینی استفاده کند.
اصولاً روی آوردن انسان به عرفان، مرحله آخر در راه شناخت ناشناختهها است. اگر انسان با هیچ یک از ابزارهای علمی یا عقلِ سَلیمی نتواند خودش را راضی کند که به شناخت کافی درباره جهان یا خداوند رسیده، به عرفان روی میآورد. این مختص به مومنان یا افرادی غیر-علمی نیست. خیلی از دانشمندان نیز در صورت ناراضی بودن از یافتههای خودشان، به عرفان روی میآورند. کسانی مثل ریچارد فاینمَن، که یک فیزیکدان برجسته و برنده جایزه نوبل بود، از جمله کسانی بودند که به نوعی عرفان معتقد بود. البته عرفان او مخلوطی از علم و هیپیگری بود. حتی این شامل خودِ کانتور نیز میشود. او در مراحل آخر زندگی خودش به این نتیجه رسیده بود که نیازی به اثبات ریاضی فرضیه پیوستار ندارد، زیرا این چیزی است که از طرف خداوند به او منتقل شده و تنها وظیفه او ارائه آن به بقیه انسانها است.
ولی نباید این تصور به خواننده دست دهد که این کتاب درباره عرفان است، و گرنه مترجم سراغ ترجمه چنین کتابی نمیرفت. این کتاب درباره بینهایتِ ریاضی، فرضیه پیوستار، و مبانی ریاضیات است، که برای روشنتر شدن تاریخِ شناختِ بینهایت، گریزی هم به اصول کابالا زده.
اصلاً بینهایت یعنی چه؟ در جواب به این سئوال خیلیها میگویند ”بینهایت یعنی بیپایان!“ خب بیپایان یعنی چه؟ اصلاً پایان چیست؟ ... سئوالاتی از این قبیل همیشه درباره بینهایت مطرح میشود، سئوالاتی که گفتن آنها ظاهراً ساده است، ولی وقتی کسی وارد مباحث مربوط به آنها میشود، جوابهای مبهمی در مقابل او قرار میگیرد. بینهایت موضوع بسیار پیچیدهای است. مترجم شخصاً نمیتواند چیزی غامضتر از این موضوع را مثال بزند. ظاهراً بینهایت جزء آن چیزهایی نیست که باید برای انسان قابل درک باشند، به همین دلیل، یکی از یگانه صفاتی که در اکثر ادیان به خداوند نسبت میدهند نامتناهی بودن اوست. هر چند انسان میتواند به آن نزدیک شود و به نوعی درک اجمالی از آن برسد.
تفکر عمیق درباره بینهایت میتواند برای انسان مشکلزا باشد. اگر این نوع غور کردنها از جنس مراقبههای عرفانی باشد، به دلیل اینکه معمولاً شخص عقلِ سلیم را کنار گذاشته و وارد دنیای دیگری میشود، ممکن است فشارهای زیادی به مغز او وارد شود. ولی به دلیل سخت بودن مسائل مربوط به بینهایت، حتی اگر آن شخص یک ریاضیدان هم باشد، این مشکلات میتواند گریبان او را نیز بگیرد. نمونه واضح آن کسانی مثل خودِ کانتور و گودل هستند، که قسمت عمده مشکلات روانی آنها به کلنجار رفتن با بینهایت و فرضیه پیوستار نسبت داده میشود.
اصطلاح معروفی هست که میگویند ”فلانی مغزش هنگ کرده“. اصولاً هنگ کردن (hanging) یک اصطلاح نرمافزاری است و هنگامی روی میدهد که یک برنامه کامپیوتری به حلقهای وارد میشود که نمیتواند از آن خارج شود و مدام یک کار را تکرار میکند. اگر یک دستگاه برای مدتی طولانی در حالت هنگ بماند، ممکن است به دستگاه آسیب بزند. معمولاً برای خارج کردن یک دستگاه از حالتِ هنگ (شامل کامپیوترهای معمولی، دستگاههای موبایل، تلویزیونهای هوشمند، و ...) باید آنها را reset، یا خاموش/روشن کرد. هنگ کردن کامل انسانها تقریباً نادر است، زیرا به دلیل نیاز به خوردن و آشامیدن، یا محرکهای خارجی، مانند سر و صدا، آنها خواه و ناخواه از حالتِ هنگ خارج میشوند. ولی ممکن است دوباره وارد چنین حالتی شوند. روشن است که تکرار چنین وضعیتهایی موجب تحلیل رفتن قوای جسمی و روحی انسان میشود.
موضوع بینهایت که در کتاب حاضر و همچنین در کتاب ”مقدمهای بسیار کوتاه درباره بینهایت“ به آنها پرداخته شده بیشتر جنبه ریاضی دارد و برای دریافت یک درک اجمالی از این موضوع طراحی شدند.
این کتاب در رده عمومی طبقه بندی میشود و پیشنیاز مطالعه آن در حد دانستن ریاضیات دبیرستانی است. این کتاب میتواند برای کسانی که به ریاضیات، تاریخ علم، و فلسفه علاقه دارند جالب باشد.
 درباره نویسنده
درباره نویسندهآمیر دان اکزل (Amir Dan Aczel) (1950-2015) ریاضیدان و مورخ آمریکایی-اسرائیلی بود. او در سال 1979 دکترای خودش را از دانشگاه اورگون آمریکا دریافت کرد، اکزل در خیلی از دانشگاههای معتبر دنیا تدریس کرد، از جمله در دانشگاه برکلی کالیفرنیا، ماساچوست، ایتالیا، و یونان. مواردی که او تدریس کرده شامل آمار و تاریخ علم میشود. بیشتر کتابهای او در زمینه ریاضیات و فیزیک هستند، از جمله معمای قطبنما، درهمتنیدگی کوانتومی، آخرین قضیه فرما، و در جستجوی صفر. تعدادی از کتابهای او، از جمله درهمتنیدگی کوانتومی، به فارسی هم ترجمه شده.
متاسفانه این ریاضیدان خوب و مروجِ علم، به علت ابتلاء به سرطان در سال 2015 در سن 65 سالگی فوت شد.
تابستان 1404
کامران بزرگزاد ایمانی
در اواخر قرن نوزدهم، یک ریاضیدان بااستعداد در یک تیمارستان بستری بود. بزرگترین دستاورد او، که حاصل مجموعهای از بصیرتهای درونی بود، درک پیشگامانه او از ماهیت بینهایت بود. این کتابی است درباره داستان زندگی گئورگ کانتور: بازتاب کارهایش، و اینکه چگونه به ایدههایش دست پیدا کرد،همان ایدههایی که در نتیجه آنها بینش فعلی ما از جهان شکل گرفته.
نظریه کانتور درباره بینهایت به خاطر داشتن تناقضهای ظاهری فراوانش مشهور است؛ برای مثال، میتوانیم ثابت کنیم که روی خطی به طول یک سانت، به همان تعداد نقطه وجود دارد که روی خطی به طول یک کیلومتر؛ همچنین میتوانیم ثابت کنیم که در طول کُل زمان، به تعداد روزها، سال وجود دارد. طبق نظر کانتور، مجموعههای بینهایت با هم برابرند.
کارهای کانتور، که عمیقاً پیچیده و فلسفی هستند، ریشه در ریاضیات یونان باستان و عدد شناسی یهودی دارند، چیزهایی که در آثار عرفانی موسوم به کابالا (Kabbalah) آمدهاند.
کانتور برای اشاره به عدد مرموزی که مجموع اعداد صحیح مثبت است، از اصطلاح الف استفاده کرد (א اولین حرف الفبای عبری است، با تمام تداعیهای الهی مرتبط با آن). א آخرین عدد مثبت نیست، زیرا ... اساساً هیچ عدد آخری وجود ندارد. همانطور که، مثلاً قبل از عدد 1 هیچ کسرِ آخری وجود ندارد و کسور کوچکتر از 1 مرتباً به آن نزدیک میشوند، א نیز آن عدد غایی است که همیشه به آن نزدیک میشویم.
ایده این کتاب حدود بیست و پنج سال پیش، یک شب دیروقت، در ذهنم جوانه زد. در آن موقع با دوستم باب ترنت، دانشجوی کارشناسی ارشد ریاضیات در دانشگاه برکلی کالیفرنیا صحبت میکردم، هر دو از فرط خستگی با نوشیدن چندین فنجان قهوه جان سالم به در برده بودیم. در آنجا باب گفت: «ببین، میخواهم چیزی را به تو نشان دهم» و شروع به نوشتن دنبالهای از نمادها کرد:
1, 2, 3, … , ω+1, ω+2... , 2ω ... , ω2, ... ωω, ... و غیره
من مجذوب این ایده شده بودم که اعداد طبیعی میتوانند فراتر از بینهایت ادامه داشته باشند، و ما واقعاً میتوانیم در مورد سطوح مختلفِ بینهایت صحبت کنیم، سطوحی که هربار بزرگ و بزرگتر میشوند و این روند پایانی ندارند. من مجذوب پارادوکسهایی شدم که باب در مورد غیرممکن بودن بزرگترین بینهایت، یا وجود مجموعهای شامل همه مجموعهها، برایم توضیح میداد. من میدانستم که این موضوعات قلب ریاضیات مدرن هستند.
سپس داستان زندگی پررنج مردی را فهمیدم که برای اولین بار ایدههای مربوط به بینهایتِ واقعی و فرضیه پیوستار را مطرح کرده بود. من مجذوب موضوعاتی شدم که درباره زندگی گئورگ کانتور یادگرفته بودم. سالها بعد، وقتی این داستان را برای ناشر کتابهایم، جان اوکس، تعریف کردم، او پیشنهاد داد که کتابی در مورد آن بنویسم. از جان به خاطر تشویق من برای دنبال کردن این موضوع در پنج سال گذشته، و از صبر و حمایت بیدریغش در طول سالهای تحقیق و نوشتن این کتاب سپاسگزارم.
از پروفسور دنیل روبرمن، رئیس دانشکده ریاضی دانشگاه برندایس، به خاطر اینکه اجازه داد در حین نوشتن این کتاب، به عنوان محقق مهمان در رشته ریاضیات، در آنجا بمانم سپاسگزارم. از کتابداران دانشگاه برندایس و کالج بنتلی به خاطر سفارش بسیاری از اسناد، مقالات و کتابهای مهم مرتبط با کار گئورگ کانتور و مفهوم بینهایت، سپاسگزارم.
مایلم از ریاضیدانانی که سخاوتمندانه وقت خود را در اختیار من گذاشتند و برای تهیه کتاب حاضر به مصاحبه شدند، مراتب قدردانی عمیق خود را ابراز کنم. این افراد شامل پروفسور آکیهیرو کاناموری از دانشگاه بوستون، پروفسور جان داوسون از دانشگاه ایالتی پنسیلوانیا و پروفسور سحارون شیلاه از دانشگاه عبری هستند.
آمیر د. آکزل
א0
در ۶ ژانویه ۱۹۱۸، مردی لاغر و خسته بر اثر نارسایی قلبی در کلینیک اعصاب هاله، که یک کلینیک روانی دانشگاهی در شهر صنعتی هاله (Halle) آلمان بود، درگذشت. جسد او بیسروصدا برای دفن در یک گورستان کوچک از میان شهر گذشت. تنها تعداد اندکی، شامل همسر و پنج فرزند بازماندهاش، در مراسم او شرکت کردند.
این گورستان حالا دیگر وجود ندارد، زیرا از آن زمان تاکنون تخریب شده تا از زمین آن برای ساخت خانههای شخصی استفاده شود. اما شخصی سنگ قبر کانتور را نجات داد و سالها بعد این سنگ بدون انتقال جسد به گورستان کوچک دیگری در هاله منتقل شد، جایی که هنوز هم میتوان آن را دید. نوشتهای که روی این سنگ حکاکی شده به این شرح است:
دکتر گئورگ کانتور
استاد ریاضی
1845/3/3 - 1918/6/1

سنگ قبر کانتور
گئورگ کانتور تا زمان مرگش، هفت ماه بود که در بیمارستان روانی هاله بستری بود. اما این اولین باری نبود که او در این کلینیک بستری میشد. گئورگ کانتور بارها در این کلینیک بستری، مرخص، و دوباره بستری شده بود. مشکلات روانی او سالها قبل از ساخت این کلینیک در سال ۱۸۹۱ آغاز شده بود.
گئورگ کانتور در سال ۱۸۶۹ دکترای خود را در رشته ریاضیات از دانشگاه برلین دریافت کرد، جایی که زیر نظر برخی از بزرگترین ریاضیدانان جهان تحصیل کرد و ایدههای مهم زیادی را در ریاضیات فرا گرفته بود. او مشتاق بود تا برای توسعه نظریههای جدید، دانش خود در زمینه آنالیز ریاضی را به کار گیرد. این جوان بیست و چهار ساله به این امید که زمان کافی برای دنبال کردن تحقیقاتش را داشته باشد از احتمال به دست آوردن اولین سمت آموزشی خودش در یک دانشگاه آلمانی هیجانزده بود. اما پس از فارغالتحصیلی، تنها پیشنهادی که برای تدریس به کانتور داده شد از دانشگاه فریدریش در هاله، حدود هفتاد مایلی جنوب غربی برلین، بود.
هاله شهری قدیمی با خیابانهای سنگفرش قرون وسطایی است. این شهر در اواسط قرن دهم به عنوان مرکز تولید نمک در کنار رودخانه سال (Saale) تأسیس شد. این شهر از بمبارانهای جنگ جهانی جان سالم به در برد و هنوز هم بسیاری از ساختمانهای قدیمی در مرکز تاریخی شهر پابرجا هستند، جایی که مردم بدون مزاحمت وسایل نقلیه موتوری، به مغازهها و کافهها میروند.
هاله، شهر پنج برج نامیده میشود. چهار منارهی کلیسای قرون وسطایی Marktkirche بر فراز ساختمانهای پایینتر در مرکز شهر خودنمایی میکنند و در نزدیکی آن، پنجمین برج، به نام برج سرخ ۱۴۱۸ قرار دارد، که یک بنای یادبود برای مبارزات مردم شهر برای استقلال از اشرافیون ستمگر است.
در سال ۱۶۸۵، موسیقیدانی بنام گئورگ فریدریش هندل (Georg Friedrich Handel) در خانهای که قدیمیترین دیوارهای پابرجای آن به قرن دوازدهم برمیگشت، در هاله متولد شد. هندل ۱۸ سال در این خانه زندگی کرد.
این خانه اکنون به موزهای تبدیل شده که به زندگی این آهنگساز اختصاص دارد، و هنوز هم قابل بازدید است. هاله همواره شهر کنسرتها، اپرا و موسیقی مردمی بوده است.

خانه هندل
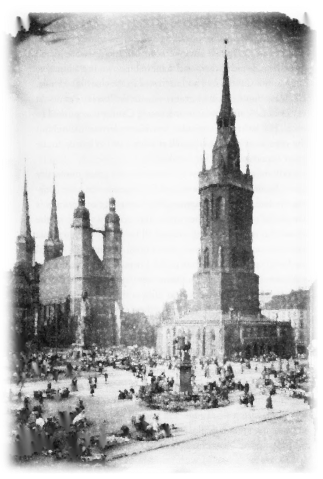
بازار هاله در حدود سالهای 1900.
مسلماً هاله باید برای کانتور جذابیت میداشت، چرا که اعضای خانوادهاش از هر دو طرف، نوازندگان بااستعدادی بودند. برخی از آنها در سرزمین مادری خود، روسیه، به شهرت رسیده بودند. اما کانتور به جذابیتهای هاله علاقهای نداشت.
خانواده او مهاجرانی بودند که از طریق دانمارک و روسیه به شبهجزیره ایبری آمده بودند، و کانتور جوان برای پیشرفت تحت فشار بود. بهویژه، پدرش در طول سالها نامههایی را برای گئورگ میفرستاد و از او میخواست که در مدرسه خوب درس بخواند و انتظارات بالای خانواده را برآورده کند.
هاله در میانه راه دو شهرِ بزرگِ دانشگاهی قرار دارد: برلین در شمال شرقی و گوتینگن در غرب. دانشگاه برلین در اواخر قرن نوزدهم بهترین دانشگاه جهان در ریاضیات بود و شهر برلین یکی از پر جنب و جوشترین و هیجانانگیزترین شهرهای تمام اروپا بود. گوتینگن قطب دیگر علمی آلمان بود. گوتینگن نیز مانند هاله، یک شهرِ قدیمی قرون وسطایی است. بسیاری از خانهها در مرکز شهر دارای پلاکهایی با نام ساکنان سابق مشهور هستند، از هاینه شاعر گرفته تا بونزن شیمیدان، اولبرز ستارهشناس، و بسیاری دیگر، که مسلماً برجستهترین آنها کارل فریدریش گاوس (۱۷۷۷-۱۸۵۵) بزرگترین ریاضیدان آن زمان است. کانتور هم جاذبه برلین، و هم جاذبه گوتینگن را حس میکرد.
اما کانتور در هاله ماند و منتظر دعوتی شد که هرگز از راه نرسید. در طول سالها، هر زمان که در برلین یا گوتینگن فرصتی برای تدریس ریاضیات پیدا میشد، به آنجا امید میبست و وقتی چنین سِمَتهایی به او پیشنهاد نمیشد، خشمگین میشد. او شخصیتی پرشور و سختگیر بود، و طبیعتی تندخو داشت. این ویژگیها باعث شد که در طول زندگی خودش دشمنانی پیدا کند و دوستانش را از خود برنجاند. برخلاف رفتارش با برخی از ریاضیدانان، کانتور در روابط خانوادگی، از خودش مهربانی و عطوفت نشان میداد.
وقتی او با همکارانش صحبت میکرد، همیشه بر وضعیت سلطه داشت، ولی در خانه نقش آرامتری را ایفا میکرد و سر میز شام به همسر و فرزندانش اجازه میداد تا سر صحبت را باز کرده و آن را جلو ببرند. او هر وعده غذایی را با این سوال از همسرش به پایان میرساند: «آیا امروز از من راضی بودی؟ آیا مرا دوست داری؟»
کانتور کارش را به عنوان یک استاد خصوصی (Privatdozent)، یعنی یک شغل دانشگاهی برای آمادهسازی ورود دانشجویان به دانشگاههای آلمان، آغاز کرد. طی چند سال کار سخت، او به دانشیاری و کمی بعد به استادی ریاضیات ارتقا یافت. کانتور درگیر تحقیقات فشرده در ریاضیات شد، اما در بحبوحه پربارترین دوره کاریاش، اتفاق عجیبی افتاد که به طور موقت به کار او پایان داد. گئورگ کانتور در تابستان ۱۸۸۴ دچار افسردگی شدیدی شد. از ماه مه، تا ماه ژوئن همان سال، او تحرک خود را از دست داد، به صورتی که قادر به انجام هیچ کاری نبود. وضعیت او باعث پریشانی همسر و فرزندانش شد و موجب شد همکارانش که او را ریاضیدانی مشتاق به رسیدن به قلههای رفیع میدیدند، گیج شوند. ولی بیماری کانتور بدون دریافت هیچ کمک حرفهای یا دارویی، بهبود یافت و به زندگی عادی بازگشت.
پس از آن، او نامهای به یکی از دوستان نزدیکش، ریاضیدان سوئدی گوستا میتاگ-لفلر (Gosta Mittag-Leffler) (1846-1927)، نوشت و در آن بیماری خود را شرح داد و اشاره کرد که درست قبل از فروپاشی روانی، روی «مسئله پیوستار» (continuum problem) کار میکرده.
سال بعد، یعنی در ۱۸۸۵، کانتور در خیابان هندل (خیابانی که به نام آهنگساز بزرگ هاله نامگذاری شده بود) خانه مجللی برای خانوادهاش ساخت. این خانه هنوز به نوه کانتور تعلق دارد. این خانه یک ساختمان دو طبقه با سقفهای بلند و پنجرههای بلند است. پدر گئورگ کانتور، که یک تاجر و دلال سهام بود، چند سال قبل فوت کرده بود و برای او نیم میلیون مارک به ارث گذاشته بود. مقداری از پول ارث صرف ساخت این خانه جدید و خرید اثاثیه شد تا خانواده کانتور بتوانند در آسایش زندگی کنند.

خانه کانتور
مانند آن زمان، امروز نیز خیابان هندل خیابانی آرام و درختکاری شده است که در آن خانههای گرانقیمت زیادی وجود دارد. خانه کانتور با پای پیاده ده دقیقه تا دانشگاه و کافهها، رستورانها و مؤسسات فرهنگی فاصله دارد. اما کانتور به اندازه کافی در خانهاش نماند تا به همراه خانواده از این خانه لذت ببرد. پس از مدت کوتاهی او دوباره بیمار شد. این بار نیز، درست قبل از بستری شدنش، کانتور روی مسئله پیوستار کار میکرد.
دانشگاه هاله یک بخش عالی روانپزشکی داشت. کانتور میتوانست بهترین درمانهای موجود آن زمان را دریافت کند - و به دلیل اینکه او استاد دانشگاه بود، این درمانها رایگان بود. دانشگاه و وزارت فرهنگ در برلین، که تمام این تصمیمات را تصویب میکردند، در اعطای مرخصیهای مکرر به کانتور و معافیت او از تدریس، بسیار سخاوتمند بودند. اما با گذشت سالها، بستری شدنهای او در بیمارستان بیشتر شد.
در بایگانی دولتی پروس در برلین، نامهای به تاریخ ۲۹ آگوست ۱۹۰۲ در مورد بودجههای ارسالی وزارت فرهنگ به وزارت دارایی وجود دارد. در این نامه وزیر فرهنگ در صورت عدم بهبود پروفسور کانتور، برای حمایت از انتصاب استاد جایگزین در دانشگاه هاله، درخواست تخصیص ۶۶۶۰ مارک را کرده بود. اما کانتور دوباره بهبود یافت و به تدریس بازگشت.
ظرف یک سال او دوباره بیمار شد و در ۱۷ سپتامبر ۱۹۰۴ دوباره در کلینیک عصبی بستری شد و تا ۱ مارس ۱۹۰۵ در آنجا ماند . سپس در پاییز همان سال، کانتور دوباره به کلینیک بازگشت.
کلینیک اعصاب هاله (Halle Nervenklinik) مجموعهای از یازده ساختمان است که در یک محوطه بزرگ حصارکشی شده قرار دارند. کیفیت ساخت و ساز آنقدر بالا بود که امروزه این مرکز تقریباً مانند زمانی که بیش از یک قرن پیش ساخته شده بود، به نظر میرسد. ساختمان اصلی، با برج نوکتیزش، بیشتر شبیه یک ستاد نظامی است تا یک کلینیک روانی. در داخل ساختمان اتاقهای جادار با پنجرههای بزرگ و حمامهای خصوصی قرار دارند. این بیمارستان جایی نبود که بیماران با دیوارهای تنگ و باریک محصور شوند. این مکان کلینیکی بود برای اقامتهای چند ماهه افراد ثروتمندی که خانوادههایشان میتوانستند هزینه اتاق، غذا، و درمان آنها را بپردازند. به گئورگ کانتور، استاد دانشگاه، یک اتاق تک نفره با منظره خوب داده شد و او آزادی داشت تا تحقیقات خود را دنبال کند. درمان او عمدتاً شامل دورههایی از غوطهور شدن در وآنِ آبِ گرم بود.
و اگرچه او در حالی درگذشت که در کلینیک بستری بود، مطمئناً هیچ توجیهی برای چیزی که بعداً برتراند راسل در مورد کانتور گفته بود (در اشاره به نامهای که کانتور نوشته بود) وجود نداشت، جملهای که میگفت ”کسانی که نامه او را میخوانند، از شنیدن اینکه او در تیمارستان مرده تعجب نخواهند کرد.“
ما ماهیت دقیق بیماری کانتور را نمیدانیم. برخی از علائم گزارش شده در او شبیه علائم مرتبط با اختلال دوقطبی یا روان پریشی است. اما حالا علل این بیماری روانی به طور کلی به عوامل ژنتیکی نسبت داده میشود. ولی در اجداد کانتور هیچ مورد شناخته شدهای از این بیماری وجود نداشت.
یک حقیقت در مورد بیماری گئورگ کانتور مشخص است. حملات افسردگی او همگی به زمانهایی مرتبط بودند که او در آنها به چیزی که اکنون به عنوان «فرضیه پیوستار کانتور» شناخته میشود، فکر میکرد. او در حال تفکر در مورد یک عبارت ریاضی کوچک بود، معادلهای که در آن حرف عبری الف بکار رفته:
2א0=א1
این معادله گزارهای است درباره ماهیتِ بینهایت. بیش از 140 سال پس از آنکه کانتور برای اولین بار آن را نوشت، این معادله (به همراه خواص و پیامدهای آن) همچنان ماندگارترین راز در ریاضیات باقی مانده است.
א1
زمانی بین قرن پنجم و ششم پیش از میلاد، یونانیان بینهایت را کشف کردند. این مفهوم چنان پرقدرت، چنان نامانوس، و چنان با شهودِ انسانی مغایر بود که فیلسوفان و ریاضیدانانِ باستان که آن را کشف کردند مبهوت شدند. این کشف باعث درد، جنون، و حداقل یک قتل شد. دو هزار و پانصد سال بعد، پیامدهای آن تأثیرات عمیقی بر دنیای علم، ریاضیات، فلسفه و دین گذاشت.
ما شواهدی داریم که نشان میدهد یونانیان به دلیل پارادوکسهای آزاردهندهای که به فیلسوفی به نام زنونِ الئایی (Zeno of Elea) (۴۹۵-۴۳۵ پیش از میلاد) نسبت داده میشود، به ایده بینهایت دست یافتند. از میان این پارادوکسها، معروفترین آنها پارادوکسی است که در آن زنون مسابقهای را توصیف میکند که بین سریعترین دونده دوران باستان، یعنی آشیل، و یک لاکپشت انجام میشود. از آنجایی که لاکپشت بسیار کندتر است، او جلوتر از آشیل حرکت خودش را شروع میکند. زنون استدلال کرد که زمانی که آشیل به نقطهای میرسد که لاکپشت مسابقه را شروع کرده، لاکپشت مسافتی را طی کرده. پس از آن، زمانی که آشیل آن فاصله جدید تا لاکپشت را طی کند، لاکپشت مسافت بیشتری را طی کرده، و این بحث تا بینهایت ادامه دارد. بنابراین، زنون نتیجه گرفت که آشیلِ تندرو هرگز نمیتواند لاکپشتِ آهسته را شکست دهد. زنون از پارادوکس خود نتیجه گرفت که با فرض اینکه فضا و زمان را میتوان بینهایت بار تقسیم کرد، حرکت غیرممکن است.
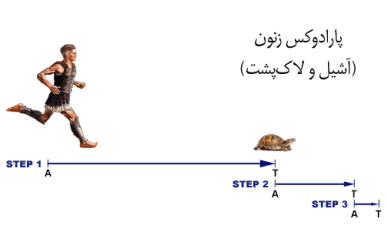
پارادوکس زنون (مسابقه میان آشیل و لاکپشت)
یکی دیگر از پارادوکسهای زنون، که دوبخشی (dichotomy) نام دارد، میگوید که شما هرگز نمیتوانید اتاقی که در حال حاضر در آن هستید را ترک کنید. زیرا ابتدا نیمی از مسافت مانده به در را طی میکنید، سپس نیمی از مسافت باقیمانده را، سپس از جایی که هستید نیمی از مسافت باقیمانده تا در را طی میکنید، و به همین ترتیب این روند را ادامه میدهید. حتی با قدمهای بینهایت زیاد – هر قدم نصف قدم قبلی است - شما هرگز نمیتوانید از در رد شوید!
پشت این پارادوکس یک مفهوم مهم نهفته است: گاهی اوقات حتی برداشتن بینهایت قدم هم میتوانند به یک مسافت کاملاً محدود منجر شوند. اگر هر قدمی که برمیدارید نصف قدم قبلی باشد، حتی اگر قرار باشد بینهایت قدم بردارید، کل مسافت طی شده دو برابر مسافت اول شما خواهد بود:
![]()
زنون از این پارادوکس استفاده کرد تا استدلال کند که با فرض تقسیمپذیری بینهایتِ فضا و زمان، هرگز حرکت حتی نمیتواند آغاز شود.
این پارادوکسها اولین نمونههای تاریخی استفاده از مفهوم بینهایت هستند. این نتیجه شگفتانگیز که تعداد نامتناهی از مراحل میتواند همچنان یک جمعِ متناهی داشته باشد، همگرایی (convergence) نامیده میشود.
میتوان با کنار گذاشتن این تصور که آشیل، یا شخصی که سعی در ترک اتاق دارد، باید گامهای کوچک و کوچکتری بردارد، سعی در حل این پارادوکسها داشت. ولی تردیدها همچنان پابرجاست، زیرا اگر آشیل باید گامهای کوچک و کوچکتری بردارد، این پارادوکسها هرگز نمیتواند به ویژگیهای نگرانکننده بینهایت، و به دامهایی که هنگام تلاش برای درک معنای فرآیندها یا پدیدههای بینهایت که در انتظار ما هستند، پاسخ دهد. اما ریشههای بینهایت در کاری نهفته است که یک قرن قبل از زنون توسط یکی از بزرگترین ریاضیدانان دوران باستان، یعنی فیثاغورث (Pythagoras) (حدود ۵۶۹-۵۰۰ پیش از میلاد) انجام شد.
فیثاغورث در جزیره ساموس (Samos)، در سواحل آناتولی متولد شد. او در جوانی به طور گسترده در همه جای جهانِ باستان سفر کرد. طبق روایات، او از بابِل دیدن کرد و سفرهای متعددی به مصر داشت، جایی که با کاهنان (حافظان اسناد تاریخی مصر از آغاز تمدن بشر) ملاقات کرد و با آنها در مورد مطالعات مصریان در مورد اعداد گفتگو کرد. پس از بازگشت، او به کروتونا در ایتالیا نقل مکان کرد و یک مدرسه تأسیس کرد که به مطالعه اعداد اختصاص داده شده بود. در آنجا او و پیروانش قضیه معروف فیثاغورث را به دست آوردند.

فیثاغورث (حدود ۵۶۹-۵۰۰ پیش از میلاد)
پیش از فیثاغورث، ریاضیدانان نمیدانستند که نتایج بدست آمده، که اکنون قضایا (theorems) نامیده میشوند، باید اثبات شوند. فیثاغورث و مکتب او، و همچنین دیگر ریاضیدانان یونان باستان، ما را با دنیای ریاضیاتِ دقیق آشنا کردند. این همان بنایی است که پله به پله با استفاده از اصول موضوعه (axioms) و منطق، ساخته میشود. پیش از فیثاغورث، هندسه مجموعهای از قوانین بود که از اندازهگیری تجربی حاصل میشد. فیثاغورث کشف کرد که میتوان یک سیستم کاملِ ریاضی ساخت، که در آن عناصر هندسی با اعداد منطبق باشند، و تنها چیزی که برای ایجاد یک سیستم کاملِ منطقی و واقعی لازم است، اعداد صحیح و نسبتهای آنها هستند. اما یک معما باعث شد دنیای ریاضی باشکوهی که فیثاغورث و پیروانش ساخته بودند درهم شکسته شود. این معما کشفِ اعداد گنگ بود.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א2
وقتی در هزاره دوم پیش از میلاد قوم بنیاسرائیل مصر را ترک کردند، مقام روحانیت یهودی تأسیس شد. اولین کسی که مقام کاهن اعظم را به دست آورد، هارون، برادر بزرگ موسی بود. کاهنان زنجیری طلایی با یک آرایه مستطیلی از دوازده مربع از فلزات گرانبها به گردن خود میآویختند که هر کدام نماد یکی از دوازده قبیله اسرائیل بود. اعتقاد بر این بود که این مدال تشریفاتی، که اوریم و تومیم (Urim veTumim) نامیده میشد، دارای قدرتهای عرفانی قوی است. اوریم وتومیم به بنیاسرائیل کمک کرد تا چهل سال مصیبت خود را در بیابان ببینند. بنیاسرائیل در مراسمی که در کوه سینا ده فرمان به آنها داده میشد، از اوریم وتومیم استفاده میکردند، سپس آن را در طول فتح سرزمین مقدس با خود حمل میکردند و در نهایت آن را در معبد اورشلیم قرار دادند. همراه با ظهور کاهنان و اوریم وتومیم، عرفان یهودی نیز متولد شد.
هزار سال بعد، هنگامی که یهودیان از تبعید خود از بابل بازگشتند، کاتبان تفاسیر رمزآلودی را برای معانی پنهانِ تورات نوشتند. این نوشتهها بسیار دقیق بودند. این تفاسیر مجازی بودند و مطالعه آنها به گروهی منتخب از محققان سپرده میشد. پس از آغاز تبعید دوم یهودیان، یعنی پس از تخریب معبد اورشلیم توسط رومیان در سال ۷۰ میلادی، این نوشتهها شرح و بسط داده شدند.
پس از این واقعه، رهبری یهود در فلسطین پراکنده شد و تعدادی از حکما در شهر یاونه ((Yavne، دور از شهر اورشلیم که آن زمان اقامت یهودیان در آن ممنوع بود، ساکن شدند. این خاخامهای اولیه جایگزین کاهنان معبد شدند و یک آکادمی آموزشی تأسیس کردند. در میان آنها کسی بود که بعدها رهبر معنوی مهمی برای یهودیان شد. این شخص خاخام یوسف بن عقیوا (Joseph ben Akiva) (حدود ۵۰-۱۳۲ میلادی) بود.
خاخام عقیوا مجموعهای از مقالات به نام «معسه مرکاوا» (Maaseh Merkava) یا «راه ارابه» نوشت. نوشتههای این خاخام، راه جدیدی را برای معنویت به مؤمنان آموخت. روش او شامل خلق تصاویر بصری از کاخهای آسمانی بود که هدف آن القای مراقبه و نزدیکی به خداوند بود.
ظاهراً خاخام عقیوا به طور اتفاقی به تمرینی برخورده بود که تقریباً برای ذهن انسان بیش از حد شدید بود. مراقبههایی که خاخام تجویز میکرد، مستلزم القای تجربیات خروج از بدن، حالات ذهنی تغییر یافته و خلسه بالایی بود که قبلاً در فرهنگ غرب شناخته شده نبود. در حالی که رؤیاهای کاخهای آسمانی در مسیر رسیدن به آن یگانه، واضح و شدید بودند، خاخام عقیوا شاگردانش را نصیحت میکرد که تسلیم توهم نشوند و درک خود از واقعیت را از دست ندهند. او نوشت: «وقتی وارد سنگهای مرمر خالص میشوید (مرحلهای از مراقبه)، نگویید 'آب! آب!' زیرا مزامیر داوود به ما میگوید : 'کسی که دروغ میگوید، در برابر چشمان من استوار نخواهد شد.'»
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א3
از اوایل سالهای ۱۶۰۰ تا اوایل سالهای ۱۸۰۰، دو ریاضیدان به کشفیات عمیقی در مورد ماهیت بینهایت دست یافتند. کشفیات آنها را میتوان ادامه بینشهای تیزبینانه ریاضیدانان یونانی دانست که دو هزار سال قبل از آنها زندگی میکردند. نظریه حسابان، و همچنین سایر حوزههای مهم ریاضیات در این دوره توسعه و پیشرفت کردند و برخی از بزرگترین نامها در ریاضیات تأثیر خود را بر این حوزه گذاشتند، کسانی مانند نیوتن، لایبنیتس، گاوس، اویلر و دیگران. با این حال، هیچ یک از این ریاضیدانان جرأت سر و کله زدن با بینهایت را نداشتند. در آن زمان ریاضیدانان وقتی یک کمیت به بینهایت نزدیک میشد، یا جایی که کمیتها به صفر نزدیک میشدند، در استنتاجهای خود از استدلالهای هوشمندانهای استفاده میکردند. بنابراین، این ریاضیدانان فقط با بینهایتِ بالقوه سر و کار داشتند. هیچکدام از آنها جرأت ورود به باغ مخفی (یعنی بینهایتِ واقعی) را نداشتند.
افتخار کشف ویژگی مهم بینهایتِ واقعی (actual infinity)، که بینهایتِ بالفعل نیز نامیده میشود، نصیب یکی از بزرگترین دانشمندان تمام دوران شد، آن شخص گالیله بود، اما او کسی نبود که عموماً با ریاضیات انتزاعی مرتبط باشد.

گالیلئو گالیله (1642-1546)
گالیلئو گالیله (Galileo Galilei) (1642-1546) یک دانشمند بینظیر بود - یک ریاضیدان، فیزیکدان، ستارهشناس، و انسانشناس. دوران کودکی گالیله ، از بدو تولدش در ۱۵ فوریه ۱۵۶۴ در پیزا، تا نقل مکان خانوادهاش به فلورانس در سال ۱۵۷۴، سپری شد. او در ایتالیای دوره رنسانس متولد شد – همان جایی که بادهای تغییرات جدید میوزیدند و خلاقیتهای انسانی شکوفا میشد.
خانواده گالیله جوان او را برای تحصیل در رشته پزشکی به دانشگاه پیزا فرستادند. در آنجا گالیله متوجه شد که یک ریاضیدان است. او بدون اطلاع خانوادهاش یک معلم خصوصی ریاضی را استخدام کرد، که شاگرد سابق ریاضیدان افسانهای ایتالیایی، تارتالیا (Tartaglia) بود. گالیله تحت آموزش اوستیلیو ریچی، جهان زیبای معادلات و هندسه را کشف کرد. گالیله دریافت که او این استعداد را دارد تا دنیای فیزیکی اطرافش را به صورت ریاضی ببیند.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א4
حقایق مربوط به بینهایت که قبلاً توضیح داده شد، در اواخر دهه ۱۸۰۰ شناخته شده بودند، اما تعداد کمی از ریاضیدانان به آنها توجه کردند. در آن زمان، سه مرکز بزرگ ریاضیات در اروپا وجود داشت. اینها گروههای ریاضیاتِ دانشگاههای پاریس، میلان، و برلین بودند.
برلین مرکز ریاضیات برای همه ریاضیدانان آلمانی زبان بود. دانشکده ریاضیات برلین پر از ستارههای مشهور جهان در این رشته بود. در واقع، در دوره ۱۸۶۰ تا آغاز جنگ جهانی اول، برلین رهبر بلامنازع ریاضیات در جهان بود.

کارل فریدریش گاوس
در آغاز قرن نوزدهم ریاضیات آلمان با کارهای گاوس کبیر، صعود خود به سوی شهرت بینالمللی را آغاز کرد. کارل فریدریش گاوس (Carl Friedrich Gauss) کودک نابغهای بود که در سنین بسیار کم، دههها پیش از آنکه حتی مورد توجه ریاضیدانان دیگر قرار گیرد، به نتایج مهم زیادی در ریاضیات دست یافته بود. گاوس در دانشگاه گوتینگن تدریس میکرد، اما شاگردانش به تأسیس دانشکده ریاضیات در دانشگاه برلین کمک کردند. در میان آنها ریاضیدانی به نام پیتر جی. ال. دیریکله (Peter G. L. Dirichlet) (۱۸۰۵-۱۸۵۹) بود، که وفادارترین شاگرد گاوس محسوب میشد. دیریکله همیشه کتاب استادش، به نام تحقیقات حسابی (Disquisitiones)، را همراه خود داشت که حاوی ایدههای بزرگ ریاضی گاوس بود. بدین ترتیب دیریکله اکتشافات ریاضی پیشگامانه گاوس را با خود به برلین آورد، جایی که به لطف دیریکله، آنالیز ریاضی مدرن متولد شد.

پیتر جی. ال. دیریکله (۱۸۰۵-۱۸۵۹)
از میان ریاضیدانان بااستعدادی که در آنجا بودند، کسی مثل برنهارد ریمان (Bernhard Riemann) (1826-1866) بود که علاوه بر کارهای نوآورانهای که در هندسه انجام داده بود، ایده انتگرال را نیز دقیقتر کرد. کارهایی که ریمان در هندسه انجام داد، او را به بررسی مسئله بینهایت سوق داد. بینهایت بودن خطوط مستقیم در اصل دوم اقلیدس نهفته است. ریمان استدلال کرد که خطوط اقلیدس را میتوان به عنوان خطوطی نامحدود و در عین حال نابینهایت نیز تفسیر کرد.

(Bernhard Riemann) (1826-1866)
یک دایره عظیمه روی یک کره را میتوان به عنوان خطی بیکران اما محدود تفسیر کرد. دوراندیشی ریاضی ریمان آنقدر تیزبین بود که بعدها ستارهشناس بریتانیایی، سر آرتور ادینگتون گفت: "هندسهدانی مانند ریمان تقریباً میتوانست ویژگیهای مهم جهانِ واقعی را پیشبینی کند." ریمان در سن شش سالگی نشانههایی از نبوغ ریاضی را نشان داد. او در آن زمان نه تنها قادر به حل تمام مسائل حسابی بود که به او ارائه میشد، بلکه میتوانست مسائل جدیدی را برای معلمانِ مبهوت خود ارائه دهد. وقتی ریمان ده ساله بود، توسط یک معلم حرفهای، دروس ریاضی را فرا گرفت. معلم متوجه شد که راهحلهای ریمان برای مسائل از راهحلهای خودش بهتر است. ریمان در چهارده سالگی یک تقویم دائمی اختراع کرد که آن را به عنوان هدیه به والدینش داد.
ریمان پسری بسیار خجالتی بود و هنگامی که برای یک سخنرانی عمومی فرصتی پیش میآمد، سعی میکرد با آمادهسازی وسواسگونه خودش بر این خجالت غلبه کند. او در نوجوانی به فردی کمالگرا تبدیل شد که اجازه نمیداد هیچ یک از کارهایش توسط دیگران دیده شود، مگر اینکه بهترین نتیجه را دربر داشت. این تمایل به اجتناب از غافلگیری، نقش مهمی در زندگی دانشگاهی او ایفا کرد.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א5
بخش عمدهای از کارهایی که وایرشتراس، ریمان، کوالفسکی، و دیگر متخصصین آنالیز در زمینه آنالیز ریاضی انجام دادند، حول ایده مهم اعداد گنگ میچرخید. ولی این اعداد گنگ چیستند و چرا اینقدر مهم هستند؟
به محض اینکه سعی کنیم یک خط هندسی را با اعداد حسابی تطبیق دهیم، طوری که یک نقطه روی یک خط به عنوان یک عدد حقیقی منحصر به فرد در نظر گرفته شود، به طرز جادویی اعداد گنگ (irrational numbers) ظاهر میشوند. ما میدانیم که باید بتوانیم اعداد را روی یک خط مستقیم قرار دهیم، و به ایده فاصله بین دو عدد و به مفهوم تقدم نقاط (به این معنی که کدام یک از دو نقطه در مرتبه اول و کدام یک دوم است) معنا ببخشیم. ما همچنین باید بتوانیم بین اعداد و نمایش آنها به عنوان نقاط روی یک خط، جلو و عقب برویم. مثلاً اگر شش بزرگتر از چهار باشد، آنگاه نمایش هر دو عدد به صورت نقاطی روی یک پاره خط مفید خواهد بود – یعنی ما باید بتوانیم ببینیم که چهار در سمت چپ شش است و فاصله بین دو عدد را تجسم کنیم.

ما روی خط میتوانیم نقاط را به کسرها نیز مرتبط کنیم. بین 0 و 1 کسرهایی مانند 1/2, 1/4, 1/5, … و غیره قرار دارند. بین 1 و 2 کسرهایی مانند 11/2, …11/4 و غیره قرار دارند. اعداد دیگری مانند 358/719 و شبیه آنها - که همگی کسری هستند - به راحتی روی خط اعداد یافت میشوند . اما خط واقعی از فشردن کردن این اعداد روی آن به دست نمیآید. حتی با تراکم بینهایت همه کسرها و اعداد صحیح (که روی هم رفته به آنها اعداد گویا گفته میشود) روی بخشی از خط اعداد، تنها چیزی که خواهیم داشت یک الکِ پر از تعداد بینهایتی از سوراخها است، و نه یک خط ممتد و تو پر. تار و پود واقعی این خط به اعداد گنگ نیاز دارد. بدون اعداد گنگ، خطی متشکل از بینهایت نقطه خواهیم داشت، که بسیار متراکم هستند، ولی تو پر نیست، در نتیجه یک خط واقعی نخواهیم داشت.
ولی با حذف تمام اعداد گویا از خط اعداد، هنوز هم یک خط تو پر با طول-کامل برای ما باقی خواهد ماند. ولی این خط نیز بینهایت سوراخ خواهد داشت. ساختار خطِ حقیقی یک راز است: این خط بینهایت چگال و بینهایت متراکم است که ساختاری بینهایت پیچیده دارد. بولزانو فکر میکرد که آنچه باعث میشود این پیوستار در کنار هم بماند، خاصیت همبندی (connectedness) آن است، یعنی این واقعیت که هر بخشی از خط حقیقی ( یا هر بازه interval) را نمیتوان به صورت اجتماع دو مجموعه باز و گسسته از اعداد نوشت. (بازهای از اعداد که شامل نقاط پایانی خود نباشد، نمونهای از یک مجموعه باز هستند.) همانطور که کانتور به ما یاد داد، اعداد روی محور اعداد حقیقی ساختار بسیار پیچیدهتری دارند و همبندی تنها یکی از ویژگیهای آن است.
در حالی که اعداد گنگ تار و پود خط اعداد را تشکیل میدهند، اعداد گویا نیز در مجموعه اعداد گنگ متراکم هستند؛ هر چقدر هم که به هر عدد گنگ نزدیک باشید، باز هم تا رسیدن به آن بینهایت عدد گویا وجود دارد. و برعکس؛ در هر همسایگی کوچک از یک عدد گویای معین، بینهایت عدد گنگ وجود دارد. تصور ساختارِ خطِ اعداد حقیقی دشوار است.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א6
گئورگ فردیناند لودویگ فیلیپ کانتور[1] در ۳ مارس ۱۸۴۵ در سن پترزبورگ روسیه متولد شد. ریشه خانوادگی او تا به امروز در هالهای از ابهام باقی مانده است. پدر گئورگ، گئورگ ولدمار کانتور، در کپنهاگ متولد شد. از اطلاعات گذرنامه دانمارکیاش، او در سال ۱۸۰۹ متولد شده بود، اما سنگ قبر او در هایدلبرگ سال تولدش را ۱۸۱۴ ذکر کرده است. ما میدانیم که خانواده پدرش پس از محاصره کپنهاگ توسط بریتانیا در سال ۱۸۰۷ به سن پترزبورگ مهاجرت کردند و خانواده کانتور خانه و دارایی خود را در طول گلولهباران بریتانیا از دست دادند. در نتیجه، ولدمار در طول زندگی خود احساسات ضد بریتانیایی را در خود پرورش داد.

گئورگ کانتور در دوران جوانی
پدر کانتور یک پروتستان معتقد بود. مادرش، ماریا بوهم، در یک خانواده کاتولیک به دنیا آمد. آنها در سال ۱۸۴۲ در یک مراسم در سن پترزبورگ ازدواج کردند. با این حال، همانطور که از نام فامیل آنها، یعنی «کانتور»، پیداست، ما میدانیم که به احتمال زیاد این خانواده از طرف هر دو طرف (و مطمئناً از طرف پدر) ریشه یهودی داشتند. کانتور در اواخر عمرش در نامهای به یکی از دوستانش نوشت که پدربزرگ و مادربزرگ او «یهودی» بودند. دو نفر از پدربزرگها و مادربزرگها، والدین دانمارکی گئورگ ولدمار بودند: جیکوب کانتور و همسرش که نام خانوادگی قبل از ازدواجشان مایر بود. هم کانتور، و هم مایر، هر دو نامهای رایج یهودی هستند. به احتمال زیاد پدربزرگها و مادربزرگهای خانواده بوهم (خانواده مادری کانتور) نیز یهودی بودهاند.
گئورگ کانتور اولین فرزند از شش فرزند خانواده کانتور بود. برادر کوچکتر گئورگ، لوئیس، در سال ۱۸۶۳ به ایالات متحده مهاجرت کرد و در نامهای که از او در آن سال از شیکاگو به مادرش نوشته شده، این جمله را میبینیم: « ... ما از نوادگان یهودیان هستیم.» این گفته مورخ معروف ریاضیات، ای. تی. بل، مبنی بر اینکه هر دو طرف خانواده ریشه یهودی داشتهاند را تأیید میکند. این موضوع که آیا گئورگ کانتور یهودی بوده است یا خیر (چه از نظر اصالت، چه اعتقاد یا ارزشهای فرهنگی) نقش مهمی در داستان ما ایفا میکند.
به دنبال ابتلای پدر خانواده به بیماری ریوی که آب و هوای مرطوب بالتیک آن را تشدید میکرد، خانواده کانتور در سال ۱۸۵۶ به فرانکفورت آلمان نقل مکان کردند. ولی ولدمار کانتور ظرف چند سال بر اثر بیماری سل درگذشت. ولدمار در سن پترزبورگ صاحب یک شرکت عمدهفروشی بینالمللی موفق، به نام کانتور و شرکا بود که منافع تجاری آن از اروپا تا ایالات متحده و برزیل امتداد داشت. تا زمانی که او در آلمان بازنشسته شد، ثروت قابل توجهی به دست آورده بود. ولدمار در دوران بازنشستگی خودش در فرانکفورت، وقت خود را صرف نوشتن نامه به پسرش گئورگ کرد که در دبیرستان بود و بعداً در سوئیس زندگی میکرد. این نامهها به گئورگ جوان در تعیین مسیر شغلیاش کمک کرد. خانواده کانتور استعدادهای موسیقیایی قوی داشتند و اعضای خانواده سازهای مختلفی مینواختند و موسیقی تدریس میکردند. پسرعموی ولدمار، جوزف گریم، نوازنده مشهور موسیقی مجلسی در دربار سلطنتی روسیه بود. کانتور از طرف مادرش، ماریا بوهم، با جوزف بوهم، رهبر ارکستر و بنیانگذار کنسرواتوار وین، نسبت داشت. گئورگ با موسیقی و هنر بزرگ شد و نقاشیهای به جا مانده از او در کودکی، استعداد قابل توجه او را نشان میدهد. یکی از عموهای کانتور استاد حقوق در دانشگاه کازان بود، جایی که او ساز و کار حقوقی را که بعدها به شروع انقلاب روسیه کمک کرد، تدوین کرد. خانواده کانتور دوست داشتند به این اشاره کنند که یکی از شاگردان عمویشان، نویسنده نامدار روسی، لئو تولستوی، بود.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א7
کانتور در هاله یک زندگی متوسط دانشگاهی در یک موسسه درجه دو را در پیش گرفت. در جلسات دانشکده ریاضی هاله هیچ ایدهای جالبی مورد بحث قرار نمیگرفت، و هیچ گفتگوی فوقالعادهای با سخنرانان مهم در مورد موضوعات تحقیقاتی جدید و هیجانانگیز وجود نداشت.
در همین دوران کانتور با والی گوتمن (Vally Guttmann)، دوست خواهرش که از یک خانواده یهودی برلینی بود، ازدواج کرد. آنها در برلین با هم آشنا شده بودند و چند سال پس از نقل مکانشان به هاله، در سال ۱۸۷۵، ازدواج کردند. آنها با حقوق ناچیز دولتی کانتور، که به طور قابل توجهی کمتر از حقوق دانشگاه برلین بود، تشکیل خانواده دادند. اما در همینجا، در شهر کوچکی در حومه آلمان بود که کانتور یک نظریه ریاضی کامل را توسعه داد که تمام آن به خودش تعلق داشت.
در جامعهای از ریاضیدانان خوب، تحقیقات ریاضی به بهترین شکل انجام میشود. نتایج تحقیقات را میتوان به اشتراک گذاشت و ایدهها را رد و بدل کرد، به طوری که نظریههای جدید بتوانند توسعه یابند و شکوفا شوند. کار کردن در انزوا سخت و کند است، و کوچههای بنبست زیادی وجود دارد که یک ریاضیدان میتواند در آنها گم شود. اما گئورگ کانتور به نحوی توانست یکی از شگفتانگیزترین نظریههای تاریخ تمدن را (به تنهایی) ارائه دهد.
کانتور ایدههای قدرتمند و مهمی را در آنالیز ریاضی با خودش به هاله آورد، ایدههایی که آنها را در برلین از کارل وایرشتراس آموخته بود. در درسهای وایرشتراس در مورد نظریه توابع، که یکی از بهترین درسهای ریاضیات ارائه شده تاکنون است، کانتور با مفاهیم منحصر به فردی آشنا شد. وایرشتراس تکنیکی را که به دنبال ایدههای بولتزانو در مورد حدها و دنبالههای نامتناهی بود، شرح داد و تعریفی روشنگرانه از یک کشف قدیمی ارائه داد، و آن اعداد گنگ بود. رویکرد بولتزانو-وایرشتراش به اعداد گنگ بر اساس حدود و ویژگی فضاهایی بود که این دو نفر به طور مستقل کشف کرده بودند، ویژگیهایی که بیان میکند یک دنباله نامتناهی در یک فضای کراندار، یک نقطه حدی در فضا است.
در چارچوب نظریه بولزانو-وایرشتراش، که بر اساس ایدههای یونانیان باستان ساخته شده، ما یک عدد گنگ را به عنوان حد اعداد گویا تعریف میکنیم. فاصله از اعضای دنباله تا عدد گنگی که به عنوان نقطه حد عمل میکند، به طور مداوم کاهش مییابد. این مکانیسم مشابه ساز و کار ذاتی پارادوکس زنون در مورد شخصی است که هرگز نمیتواند از اتاق خارج شود. شخص نیمی از مسافت را تا در اطاق، سپس نیمی از مسافت باقی مانده و به همین ترتیب تا بینهایت را طی میکند. در اینجا، میتوان در را به عنوان نشان دهنده یک عدد گنگ، یا حدِ یک دنباله نامتناهی از اعداد گویا در نظر گرفت.
در مدتی که کانتور در برلین بود، آثارش تحت تأثیر سنت وایرشتراس باقی ماند. در همین راستا، او در هاله آنالیز ریاضی را دنبال کرد. وایرشتراس، معلمِ پیرِ دبیرستان که هوش و ذکاوتش برای او مقام استادی به همراه داشت، به انتشار نتایج کارهایش اعتقادی نداشت و حتی دوست نداشت که دانشجویانش در کلاس یادداشتبرداری کنند. یکی از دلایلی که آثار او باقی مانده این است که یکی از دانشجویان سوئدی او، که بعدها به نوبه خودش ریاضیدان مهمی شد و به دوست خوبی برای کانتور بدل گشت، پس از بازگشت به استکهلم، یادداشتهای دقیقی از آنها برداشت و آنها را سازماندهی کرد. این دانشجو گوستا میتاگ-لفلر (Gosta Mittag-Leffler) (1846-1927) بود.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א8
ریاضیدان مشهور فرانسوی، هنری پوانکاره (Henri Poincare) (1854-1912) گفته بود که نظریه مجموعههای کانتور یک طاعون است، یک بیماری واگیردار که روزی شَر آن از سر ریاضیات کم خواهد شد. ولی درمقابل، ریاضیدان برجسته آلمانی داوید هیلبرت، در پاسخ گفت که "هیچ کس ما را از بهشتی که گئورگ کانتور برای ما گشوده است، بیرون نخواهد کرد." در واقع ورود کانتور به این باغ بهشتی بیکران، دوران جدیدی را در ریاضیات گشود. همانطور که دانته توصیف کرده بود، دنیای اسرارآمیز بینهایتِ بالفعل را میتوان با تصور دایرههایی که درون دایرههای دیگر قرار گرفتهاند، تجسم کرد. هر دایره نشاندهنده یک جایگاه والاتر است (به عبارتی، مرتبه بالاتری از بینهایت). پایینترین شکل همه این بینهایتها، سطحی از بینهایت است که توسط اعداد طبیعی ۱، ۲، ۳ و غیره اشغال شده است.
اعداد طبیعی حتی اگر نامتناهی باشند، ولی حداقل میتوان آنها را شمرد. این فرآیند شمارش است که اهمیت دارد ، نه خود شمارش، زیرا چنین شمارشی هرگز پایان نخواهد یافت. اعداد طبیعی را میتوان شمرد، زیرا میتوان آنها را یکی پس از دیگری، ۱، ۲، ۳، ۴، ... و غیره نام گذاری کرد. بنابراین، هرچند اعداد طبیعی نامتناهی هستند، آنها قابل شمارشند (countable). کانتور در اوایل دوران حرفهای خودش از یک استدلال هوشمندانه برای نشان دادن اینکه اعداد گویا نیز قابلشمارش هستند، استفاده کرد. بنابراین، همانطور که گالیله نشان داده بود که به تعداد اعداد صحیح، مربع اعداد صحیح وجود دارد، کانتور نیز نشان داد که به تعداد اعداد صحیح، اعداد گویا وجود دارد. این استدلال، به اثبات قطری کانتور (Diagonalization Proof) برای شمارشپذیری اعداد گویا معروف است.
کانتور اولین بار در سال ۱۸۷۴ از این اثبات استفاده کرد، اما بعداً، در سال ۱۸۹۱، این اثبات را بهبود بخشید زیرا نگران تعدادی از پیامدهای فنی بود که در سال ۱۸۷۴ برای او روشن نبود. او فکر میکرد که این اثبات میتواند به اندازه کافی قدرتمند شود تا به او اجازه دهد سلسله مراتبِ کاملی از اعداد ترامتناهی را بنا کند. همانطور که در زیر نشان داده شده است،کانتور اثبات خود را با مرتب کردن تمام اعداد گویا در یک آرایه دو بعدی آغاز کرد.

همانطور که نشان داده شده است، ادامه فلشها در شکل بالا از عددی به عدد دیگر، یک تناظر یک به یک از اعداد گویا به تمام اعداد طبیعی ایجاد میکند. در اینجا 1/1 با 1 جفت شده است؛ 2/1 با 2 جفت شده است؛ 1/2 با 3 جفت شده است؛ 1/3 با 4 جفت شده است ... و به همین ترتیب.
بنابراین هر عدد گویا در مقابل یک عدد طبیعی قرار دارد و درنتیجه شمرده میشود (حتی اگر افزونگیهایی وجود داشته باشد؛ برای مثال، عدد 1 که به شکل 1/1، 2/2، 3/3 و غیره ظاهر میشود، بینهایت بار شمرده میشود).
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א9
در ۲۹ ژوئن ۱۸۷۷ کانتور نامهای به ددکیند نوشت. او بسیار هیجانزده و کاملاً گیج بنظر میرسید. از نظر ریاضی او میتوانست خاصیت بینهایت را که تازه کشف کرده بود ثابت کند، اما این نتیجه برایش اصلاً منطقی نبود. در این نامه که بهطور غیرمعمول به زبان فرانسوی نوشته بود، گفت: " Je le vois, mais je ne le crois pas."، که یعنی ”میبینم، ولی نمیتوانم آن را باور کنم“. کانتور به تازگی یک ویژگی بینهایت را کشف کرده بود که حتی برای او تکاندهندهتر بود.
ایده بُعد (dimension) برای کُل ریاضیات بسیار مهم است. اقلیدس نقطه را به عنوان چیزی تعریف کرد که طول ندارد؛ خط را چیزی تعریف کرد که عرض ندارد؛ و صفحه را چیزی تعریف کرد که عمق ندارد. خط طول دارد، صفحه مساحت دارد، و یک جسم سه بعدی حجم دارد. ادامه این مفهوم به ابعاد بالاتر در ریاضیات بسیار طبیعی است، اگرچه فهمِ سه بعدی ما بیشتر از این ادامه پیدا نمیکند.

کانتور این سوال را از خود پرسید که ”مرتبه بینهایتِ اشیاء گوناگون با ابعاد مختلف چیست؟“ کانتور برای پاسخ به این سوال، به آثار ریاضیدان و فیلسوف بزرگ فرانسوی رنه دکارت (Rene Descartes) (1596-1650) متوسل شد. دکارت مشهورترین ریاضیدان زمان خود بود، دورانی که تعدادی از ریاضیدانان بزرگ مانند پاسکال، فرما و گالیله را به خود دیده بود.
رنه دکارت در ۳۱ مارس ۱۵۹۶ در لاهه، نزدیک تور فرانسه متولد شد. خانواده دکارت از اشراف بودند، اما ثروتمند نبودند. او فرزند سوم بود و مادرش پس از تولد او درگذشت. پدرش دوباره ازدواج کرد و رنه و خواهر و برادرانش توسط یک معلم سرخانه بزرگ شدند. در کودکی، به دلیل کنجکاوی زیادش در مورد جهان و اینکه همیشه میخواست بداند چرا همه چیز به این شکل است، به عنوان یک فیلسوف جوان شناخته میشد. رنه در سن هشت سالگی برای تحصیل به کالج ژزوئیتها در لافلش فرستاده شد.

رنه دکارت (1596-1650)
دکارت پسری نحیف بود و وضعیت سلامتیاش چندان خوب نبود. رئیس دانشگاه میخواست سلامتی پسر بهبود یابد، بنابراین به رنه اجازه داد صبحها تا دیروقت بخوابد و تا زمانی که تصمیم بگیرد حالش به اندازه کافی خوب است که در کلاس درس حاضر شود، در رختخواب بماند. این امتیاز برای دکارت به عادتی مادامالعمر برای ماندن در رختخواب و بررسی مسائل ریاضی و فلسفی در حالت استراحت تبدیل شد. دکارت بعدها اعتراف کرد که پایههای فلسفه و ریاضیات او در زمانی شکل گرفت بود که او وقت خودش را در کالج ژزوئیتها در رختخواب میگذراند. اگرچه او در دانشگاه زبان لاتین و یونانی، و فن بیان خواند، اما ذهن او همیشه به سمت سوالاتِ فلسفی و مسائل ریاضی متمایل بود.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א10
لئوپولد کرونکر تا سال ۱۸۷۱ به کارهای دانشجوی سابق بااستعداد خودش در دانشگاه برلین علاقهمند بود و به کانتور پیشنهاد کمک داد تا جایگاهش را در هاله تثبیت کند. کرونکر در مورد اولین مقالات کانتور که در مورد سریهای مثلثاتی و آنچه بعدها قضیه کانتور-لبگ نامیده شد، پیشنهادهایی به او داد. کانتور تحت تأثیر روشهای هوشمندانهای که توسط کرونکر ارائه شده بود قرار گرفت و صمیمانه به خاطر تمام کمکهایش از معلم سابقش سپاسگزار بود.

لئوپولد کرونکر (1823-1891)
اما هنگامی که کانتور شروع به گسترش نتایج خود کرد و توجه خود را به اعداد گنگ و بینهایت معطوف کرد، کرونکر به طور فزایندهای مضطرب شد. مشکل از یک اختلاف صرفاً فلسفی بین دو این آغاز شد. کرونکر همیشه با ایدههای آنالیز ریاضی مخالف بود و با پدرِ آنالیز، یعنی کارل وایرشتراس، بحثهای مداومی داشت.
طبق سنت، کرونکر به سادگی از باور به وجود اعداد گنگ سر باز میزد، و تحت تأثیر این واقعیت که دایرهها ناگزیر به اعدادی مثل π منجر میشوند، قرار نمیگرفت. از نظر کرونکر، فقط اعداد صحیح واقعی بودند. تمام چیزهای دیگر صرفاً حاصل تخیل بودند.
از آنجایی که امروزه هر کودکی میتواند روی یک ماشین حساب کلید جذر را فشار دهد و جذر عددی مثل 2 را به دست آورد (بسط اعشاری بیپایان این عدد گنگ پس از تعداد محدودی از ارقام کوتاه شده و بصورت گرد نمایش داده میشوند)، ممکن است فکر کنیم که کرونکر (که به وجود چنین اعدادی اعتقاد نداشت) ریاضیدان بسیار ضعیفی بوده است. اما در واقع کرونکر ریاضیدان بزرگی بود و امروزه به خاطر تعدادی از کارهای مهم در ریاضیات شناخته میشود. همین واقعیت که او ریاضیدان بزرگی بود، اختلاف کرونکر با کانتور را بسیار چشمگیرتر میکرد. اختلافات آنها عمیق بود. کرونکر با تمام وجودش معتقد بود که هر چیزی غیر از اعداد صحیح غیرطبیعی است، و سروکار داشتن با اعداد گنگ عملی خلاف طبیعت بود. در واقع او کانتور را به دلیل تدریس چنین مفاهیمی در دانشگاه، به «فاسد کردن جوانان» متهم میکرد. کرونکر همراه با نفرتی که از اعداد گنگ داشت، از هر چیزی که حتی به طور مبهم به مفهوم بینهایت مربوط میشد نیز نفرت عمیقی داشت.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א11
طبق آنچه در فرهنگ اعداد عجیب و جالب Penguin آمده، یک گوگول (googol)، عددی است که روزی یک کودک در مهدکودک روی تخته نوشت و برابر است با:
1,0000000000,0000000000,0000000000,0000000000, 0000000000,0000000000,0000000000,0000000000, 0000000000, 0000000000.
این عدد عبات است از 1 و صد صفر جلوی آن. این همان عددی بود که کودک آن را بزرگترین عدد در جهان میدانست. ریاضیدانی به نام ادوارد کاستنر، که عموی کودکی بود که عدد بالا (گوگول) را اختراع کرد، پیشنهاد داد که میتوان عدد بسیار بزرگتری به نام گوگولپلکس (googolplex) را تشکیل داد و آن را به صورت 1 و به تعداد یک گوگول صفر جلوی آن تعریف کرد. بنابراین، یک گوگولپلکس عبارت است از 10googol است، که حقیقتاً عدد بسیار بزرگی است.
این بازی سرگرمکننده نامگذاری اعداد بزرگ، و باز هم بزرگتر، میتواند تا ابد ادامه یابد. ما میتوانیم عدد بسیار بزرگی که بصورت 10googolplex یا 10000googolplex، یا googolplexgoogolplex تعریف میشود، را پیشنهاد کنیم. ولی با این حال، ما هرگز به "بزرگترین عدد" نخواهیم رسید. دلیل آن این است که به سادگی هیچ عددی وجود ندارد که از همه اعداد بزرگتر باشد. هر عددی که داشته باشیم، تنها کاری که باید انجام دهیم این است که عدد 1 را به آن اضافه کنیم، که با اینکار عدد بزرگتری خواهیم داشت. هیچ بزرگترین عددی وجود ندارد؛ اعداد تا بینهایت ادامه دارند. برای تصور این موضوع، فقط چشمانتان را ببندید و خود را در حال پرواز در فضا تصور کنید. روبرویتان، اعدادی را میبینید که مانند تابلوهای فاصله در یک بزرگراه به سمتتان سرازیر میشوند: ۱۱۳۸، ۱۱۳۹، ۱۱۴۰... ۲۵۶۷، ۲۵۶۸، ۲۵۶۹، ۲۵۷۰... با این تفاوت که همیشه و تا ابد اعداد بیشتری وجود دارند.
نبوغ گئورگ کانتور این بود که او (همراه با بولتزانو و احتمالاً گالیله) جزو اولین ریاضیدانانی بود که به تخیل خود اجازه داد آزادانه حرکت کند و مفهومِ بیپایانی او را از تلاش باز نداشت. ممکن است محققان مذهبی که کابالا و الهیات مسیحی را مطالعه میکنند، در تلاش برای تصور عظمتِ بیپایانِ الهی چنین شجاعتی را تجربه کرده باشند. مطلقِ کانتور و اعداد فرامتناهی او شباهتی به تصویر خدا دارند که توسط آگوستینِ قدیس در کتاب «شهر خدا» توصیف شده است. آگوستین مینویسد: «هر عددی برای او شناخته شده است که فهم او را نمیتوان شمرد. اگرچه سلسله نامتناهی اعداد را نمیتوان شمرد، اما این بینهایت خارج از درک او نیست. در نتیجه هر بینهایتی ، به شکلی که ما نمیتوانیم آن را بیان کنیم، برای خدا چیزی محدود است.»
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א12
کانتور اکنون مشتاق مشخص کردن الفها و روابط بین آنها بود. او تازه دروازه باغ جادویی اعدادِ ترامتناهی را باز کرده بود و چیزی که حالا میخواست بداند، ترتیب آنها بود. کانتور میدانست که کوچکترین مرتبه بینهایت، یعنی کوچکترین عدد ترامتناهی، الف-صفر (0א) است. او با یک قضیه شگفتانگیز که در دهه 1870 ثابت کرده بود همچنین میدانست که برای هر مجموعهای، هر چه که باشد، همیشه یک مجموعه بزرگتر وجود دارد، و آن مجموعه زیرمجموعههای مجموعه اصلی است. به عنوان مثال، بیایید به مجموعه سه عدد {1، 2، 3 } نگاه کنیم. مجموعه تمام زیرمجموعههای این مجموعه سه عضوی چیست؟ این مجموعه که مجموعه توانی (power set) مجموعه اصلی نامیده میشود، شامل تمام زیرمجموعههای ممکنی است که میتوان از مجموعه سه عضوی تشکیل داد. اینها عبارتند از: {}، یا همان مجموعه تهی؛ سه مجموعه از هر کدام از عضوها، {1}، {2}، {3}؛ سپس مجموعه جفتها، {1، 2 }، {1، 3}، و {2، 3}؛ و در نهایت، مجموعه تمام عضوهای مجموعه اصلی، {1، 2، 3}. بنابراین، مجموعه توانی یک مجموعه سه عضوی، هشت عضو دارد. تعداد عضوها به صورت زیر بدست میآید: 23=8. به طور کلی، قاعده این است که هر عضو در مجموعه اصلی دو احتمال وجود دارد: قرار گرفتن در یک زیرمجموعه یا قرار نگرفتن در زیرمجموعه، بنابراین 23=8 زیرمجموعه ممکن از یک مجموعه سه عضوی وجود دارد.
کانتور میدانست که مجموعه تمام اعداد حقیقی، یا همان پیوستار (continuum) خطِ حقیقی، شامل تمام زیرمجموعههای ممکن از مجموعه تمام اعداد صحیح است. هر عدد صحیح میتواند در هر یک از مکانهای نامتناهی یک عدد اعشاری قرار گیرد یا قرار نگیرد. از این رو، تعداد عناصر پیوستار باید 2 به توانِ تعدادِ نامتناهی اعداد صحیح باشد. بنابراین، عدد اصلی پیوستار
0א c=2 خواهد بود. برای دیدن این موضوع راه آسانتری وجود دارد.
روی پیوستار اعداد حقیقی، هر عدد یک بسط اعشاری نامتناهی دارد. هر عدد در امتداد متراکم اعداد روی خط، با تعداد نامتناهی عدد صحیح (اما به طور قابلشمارش) از 0 تا 9 نمایش داده میشود. در هر یک از تعداد نامتناهی مکانهای قابل شمارش برای یک عدد، یک و فقط یک رقم وجود دارد: 0، 1، 2 ... و غیره. اما ما میدانیم که پایههای سیستمهای عدد نویسی میتوانند تغییر کنند. برای ساده کردن موضوع، اگر پایه عدد نویسی ما عدد 2 باشد، هر عدد روی خط حقیقی را میتوان با یک دنباله نامتناهی از 0ها و 1ها نوشت (یعنی، ما تمام اعداد خود را در پایه 2 مینویسیم). بنابراین، برای هر عدد معین، در تمام مکانها، دو انتخاب برای رقم وجود دارد: 0 یا 1. برای هر عدد، به تعداد الف- صفر چنین مکانهایی وجود دارد. بنابراین، تعداد اعداد روی خط حقیقی (عدد اصلی پیوستار) برابر است با: 0א c=2.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א13
گفته شده که بیماری کانتور ممکن است یک اختلال دوقطبی بوده باشد، که به آن افسردگی شیداگونه نیز گفته میشود. برخی از روانشناسان حتی در رفتار او نشانههایی از عقدهِ آزار و اذیت دیدهاند. در سال ۱۹۳۷، یی. تی. بل (E. T. Bell)، با استفاده از یک رویکرد فرویدی، رابطه گئورگ کانتور با پدرش در دوران کودکی را ردیابی کرد. بل استدلال کرد که رابطه بین یک پسر حساس که میخواهد والدینش را راضی نگه دارد و یک پدر مستبد که تمام رفتارهای فرزندش را به او دیکته میکند، قطعاً باعث مشکلات روانی کودک میشود. بل نتیجه گرفت که افسردگی کانتور نتیجه رابطه با پدرِ سختگیرش بوده است.
محققان بعدی معتقد بودند که دورههای افسردگی و سایر علائم کانتور نتیجه شکستهای ناامیدکننده او در اثبات فرضیه پیوستار بوده که با عذاب بیرحمانهای که کرونکر بر او تحمیل میکرد، تشدید شده بود. این متخصصان نقش پدر کانتور را نادیده میگیرند، ولی روانشناس و ریاضیدانی به نام ناتالی چارود (Nathalie Charraud) که این مسئله را مطالعه کرده بود، تا حدودی به استدلالهای بل اعتبار میبخشد.
ما امروزه میدانیم که اختلال دوقطبی صرفاً « ناشی از» یک رویداد در زندگی بیمار نیست. عوامل ژنتیکی در ایجاد این بیماری نقش دارند و تاثیر عوامل محیطی نیز ممکن است به سادگی ناامیدی ناشی از تلاش برای حل یک مسئله، یا آسیب ناشی از انتقادات همکاران نباشد. حتی زمانی که بیمار در دسترس است، قضاوت در مورد دلایل یک بیماری روانی دشوار است. تلاش برای انجام این کار برای فردی که بیش از یک قرن از مرگش میگذرد، و بدون دسترسی به سوابق کامل بالینی او، بسیار دشوارتر است.
اما روانشناسی مدرن دریافته است که افسردگی زمانی میتواند ایجاد شود که فرد با مشکلات برطرف نشدنی روبرو شود. صرف نظر از علت بیماری روانی کانتور، شکست او در اثبات فرضیه پیوستار و خشم و ناامیدی او از رفتار کرونکر، باید علت اصلی وضعیت او بوده باشد. ما این را بر اساس اولین فروپاشی روانی کانتور، و نیز از نحوه توصیف وضعیت عاطفی خودش در آن زمان برای دوستان و همکارانش میدانیم.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א14
کانتور متوجه شد که اگر بخواهد فرضیه پیوستار را اثبات کند، باید راهی برای مقایسه اعداد اصلی فرامتناهی خود ایجاد کند. انجام این کار ثابت میکرد که هر عدد اصلی فرامتناهی عضوی از سیستم الفها است و بنابراین خارج از این ترتیب هیچ عدد اصلی وجود ندارد: 0א، 1א، 2א، 3א، 4א، ... کانتور به دنباله الفهای خودش نام تاف (ת) را داد، که آخرین حرف الفبای عبری است. او این کار را برای اشاره به پایان انجام داد: هر عدد اصلی نامتناهی باید یک الف باشد (باید به سیستم ת تعلق داشته باشد که شامل همه الفها است.) اگرچه این سیستم تا ابد ادامه داشت - همیشه الفهای بزرگتر و بزرگتری وجود داشتند هیچ عدد اصلی نامتناهی خارج از سیستم او وجود نداشت.
اما قبل از اینکه کانتور بتواند ثابت کند که هر عدد اصلی نامتناهی جایگاه خود را در سیستم ת دارد، کانتور به روشی برای مقایسه هر جفتِ ممکن از اعداد اصلی نیاز داشت. اعداد اصلی نامتناهی باید همان اصل ترتیبی را داشته باشند که اعداد حقیقی روی خط دارند: یعنی، برای هر دو عدد از این نوع، آنها یا برابر هستند (a=b) یا یکی بزرگتر از دیگری است (a<b یا a>b). برای دستیابی به این ویژگیِ اعداد اصلی ترامتناهی، کانتور مجبور بود یک ویژگی خاص از مجموعهها را تعریف کند. ما این ویژگی را اصل خوشترتیبی (well-ordering principle) مینامیم.
اصل خوشترتیبی میگوید که هر مجموعهای میتواند خوشترتیب باشد، و مجموعهای خوشترتیب نامیده میشود که اگر تمام زیرمجموعههای غیرتهی آن، یک کوچکترین عضو داشته باشد. بیایید به یک مثال نگاه کنیم. اگر مجموعه ما {1, 2, 3} باشد، آنگاه میدانیم که مجموعه همه زیرمجموعههای آن هشت عضو دارد(همانطور که قبلاً دیدیم، 23=8). یکی از این زیرمجموعهها مجموعه تهی است و هفت زیرمجموعه دیگر عبارتند از:
{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}.
مجموعه اصلی {1,2, 3} خوشترتیب است، زیرا هر یک از زیرمجموعههای غیرتهی آن دارای یک کوچکترین عضو است. این کوچکترین عضوها، به ترتیب عبارتند از:1, 2, 3, 1, 1, 2, 1. کانتور نیاز داشت اصل خوشترتیبی را اثبات کند، یعنی ثابت کند که هر مجموعه (به ویژه مجموعههای نامتناهی) میتواند مانند مجموعه بالا خوشترتیب باشد.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א15
یک پارادوکس (تناقض) قدیمی وجود دارد که به فیلسوف قرن ششم پیش از میلاد، اِپیمنیدس کِرتی (Epimenides)، نسبت داده میشود. این مردِ کِرتی میگوید: «من دروغ میگویم.» آیا باید حرف او را باور کنیم؟ اگر حرف او درست باشد، پس او دروغ میگوید و حرفش نادرست است. اگر گفته او نادرست باشد، پس او دروغ نمیگوید و گفتهاش درست است. سَنت پُل در نامهای به تیتوس، با جمله زیر به این پارادوکس باستانی اشاره میکند: «یکی از شاعران کِرتی گفته بود که همه کرتیها دروغگو هستند.»
یکی دیگر از پارادوکسهای دوران باستان، معمای تمساح است. تمساحی کودکی را میدزدد و سپس به پدر کودک میگوید: «اگر بتوانی درست حدس بزنی که کودک را برمیگردانم، فرزندت را به تو برمیگردانم.» پدر پاسخ میدهد: «تو کودکم را برنمیگردانی.» تمساح باید چه کار کند؟
در سال ۱۸۹۷، ریاضیدان ایتالیایی، چزاره بورالی-فورتی (Cesare Burali-Forti) (۱۸۶۱-۱۹۳۱)، پارادوکسی را در نظریه مجموعههای کانتور کشف کرد. بورالی-فورتی کل توالی اعداد ترتیبی (مانند "اول"، "دوم"، "سوم" و غیره) را در نظر گرفت. او متوجه شد که این مجموعه باید شامل یک عدد ترتیبی باشد که از همه اعداد ترتیبی بزرگتر است. اما طبق تعریف، مجموعه اعداد ترتیبی باید شامل همه اعداد ترتیبی باشد و به هر یک از این اعداد میتوان یک عدد اضافه کرد. بنابراین، هیچ مجموعهای نمیتواند شامل همه اعداد ترتیبی باشد. با تعمیم ایده بورالی-فورتی، میتوان نشان داد که هیچ بزرگترین الفی نمیتواند وجود داشته باشد. کانتور در سال ۱۸۹۷ از پارادوکس بورالی-فورتی آگاه بود، زیرا آن را در نامهای به ریاضیدان دیگری ذکر کرد. در کتاب «مبانی نظریه مجموعهها» نوشته زرملو، که بر اساس کار کانتور نوشته شده است، مسئله مطرح شده توسط بورالی-فورتی با فرض بر اینکه اصلاً مجموعه همه اعداد ترتیبی وجود ندارد، حل میشود. یک پارادوکس شناختهشدهتر، که توسعه ایدههای کانتور را نیز پیچیده کرد، پارادوکس معروف راسل بود.
برتراند راسل یکی از مشهورترین فیلسوفان قرن بیستم بود. نوشتههای او در مورد آزادی سیاسی به او کمک کرد تا در سال ۱۹۵۰ جایزه نوبل ادبیات را کسب کند. راسل یک صلحطلب مشهور بود و در متافیزیک، معرفتشناسی، اخلاق و سایر زمینهها کار کرده بود. سهم راسل در ریاضیات شامل اثر معروف او، اصول ریاضیات (Principia Mathematica)، است که با همکاری آلفرد نورث وایتهد (Alfred North Whitehead) نوشت و شامل سه جلد است که بین سالهای ۱۹۱۰ تا ۱۹۱۳ منتشر شدند. این کتابهای قطور برای ایجاد یک پایه منطقی کامل برای تمام ریاضیات طراحی شده بودند. این کتاب مبنای کار تعدادی از منطقدانان مهم شدند که برای ایجاد یک نظریه منطقی و کامل از ریاضیات تلاش میکردند. در میان آنها کورت گودل (Kurt Godel) بود که بعداً با نشان دادن اینکه بنای ساخته شده توسط راسل و وایتهد به عنوان پایهای برای ریاضیات به هیچ وجه کافی نیست، دنیای ریاضیات را شگفتزده کرد.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א16
گئورگ کانتور از پارادوکسهایی که در سالهای اولیه قرن بیستم افزایش یافته بودند، دلسرد شده بود. پارادوکس راسل، و بسیاری از پارادوکسهای مرتبط با آن که توسط ریاضیدانان دیگر، چه قبل از راسل و چه بعد از او، کشف شده بودند، پایههای ریاضیات را تهدید میکردند. فرضیه پیوستار کانتور ارتباط نزدیکی با مفاهیمی دارد که در اعماق مبانی ریاضیات نهفتهاند، و بنابراین این پارادوکسها احتمال اینکه کانتور میتوانست بر مشکلاتش غلبه کند و فرضیه پیوستار را اثبات کند، کمتر میکرد.
با گذشت سالها، کانتور بیشتر در ناامیدی فرو رفت و دوره بیماری روانیاش بیشتر شد. او به مدت طولانیتری در بیمارستان روانی هاله بستری شد. در طول جنگ جهانی اول، اکثر بیماران به مراکز دیگری منتقل شدند تا برای سربازانی که مجبور بودند در شهر اسکان داده شوند، جا باز شود. در این مدت تنها دو بیمار در کلینیک روانی باقی ماندند، یکی از آنها همسر یک قاضی ثروتمند بود که به دلیل اینکه خانوادهاش نمیخواستند او به تیمارستان منتقل شود، یازده سال در آنجا مانده بود. بیمار دیگر هم گئورگ کانتور بود. سلامت عمومی کانتور به طور روشن رو به زوال بود. آنچه در ذهن او ثابت مانده بود، باور راسخ به این بود که خداوند از طریق او فرضیه پیوستار را به جهان ارائه کرده است. همچنان که کانتور از دنیای واقعی فاصله میگرفت، ذهنش به حالتی کشیده شد که دیگر نمیتوانست واقعیت و خیال را از هم تشخیص دهد.
در همان زمان، کودکی باهوش در چکسلواکی در حال بزرگ شدن بود. نام او کورت گودل (Kurt Godel) بود و شرایط خانوادگیاش کاملاً با کانتور تفاوت داشت. سرنوشت چنین رقم زد که گودل جانشین کانتور شود و به یکی از بزرگترین اندیشمندان تمام دورانها تبدیل شود.
کورت فریدریش گودل (Kurt Friedrich Godel) در ۲۸ آوریل ۱۹۰۶ - در بحبوحه سالهای پرآشوب نظریه مجموعهها، درست در میانه ارائه کونیگ در سال ۱۹۰۴، و ارائه اصل موضوع انتخاب زرملو در سال ۱۹۰۸ - در شهر برنو در موراویا، چکسلواکی (منطقهای که اکنون بخشی از جمهوری چک است) متولد شد. خانواده گودل از نظر قومی آلمانی بودند و اعضای آن نسلها در چکسلواکی و اتریش زندگی کرده بودند و پیوندهای محکمی با وین داشتند. گودل یک برادر به نام رودولف داشت که چهار سال بزرگتر بود و کورت جوان به او بسیار وابسته بود.

کورت گودل (1906-1978)
پدر کورت، رودولف، در سالهای اولیه کودکی کورت در تجارت بسیار موفق بود و ظرف چند سال توانست یک خانه سه طبقه برای خانوادهاش بسازد. دو عمه او نیز سالهای زیادی در آن خانه با خانواده گودل زندگی کردند. مادر کورت، ماریان (هاندشو)، نسبت به شوهرش از طبقه اجتماعی بالاتری بود و تحصیلات خوبی داشت. او دو پسرش را طوری تربیت کرده بود که مانند جنتلمنهای اتریشی بزرگ شوند، به این امید اینکه آنها به مجارستانیهای فرهیختهای تبدیل شوند که در هنر، موسیقی و زبانهای مختلف مهارت داشته باشند. کورت در طول کودکی خودش چندین زبان یاد گرفت، اما او به ندرت به زبان چکی، (یعنی زبان سرزمینی که در آنجا زندگی میکرد) صحبت میکرد، زیرا خانوادهاش آن را نسبت به آلمانی، زبان بیروحتری میدانستند.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א17
کورت گودل در سال ۱۹۲۴ از دبیرستان فارغالتحصیل شد و برای ثبت نام در دانشگاه به وین نقل مکان کرد. در سه سال آخر تحصیل در دبیرستان، تمرکز او بر ریاضیات بود، اما علاقه زیادی به فلسفه و فیزیک نیز نشان میداد. این سه علاقه در طول زندگیاش با او ماند. او سالهای زیادی را صرف پیوند مفاهیم جهان فیزیک با ایدههای فلسفی و کشفیات مرموزی کرد که در مبانی ریاضیات به آنها دست یافته بود.
کورت در دبیرستان بسیار خوب بود و میتوانست در هر دانشگاهی در اروپا تحصیل کند. دانشگاه برلین، با تمرکز چشمگیر ریاضیدانانِ برجستهاش، مطمئناً مکان جذابی برای این دانشجوی جوان و باهوش بود. ولی کورت به خانوادهاش بسیار وابسته بود. بنابراین تصمیم گرفت به نزدیکترین دانشگاه معتبر، یعنی دانشگاه وین، برود.
فاصله برنو تا پایتخت اتریش کمتر از هفتاد مایل است، بنابراین گودل وقتی در وین بود، به خانهاش نزدیک بود. این شهر نیز برای او جذابیتهای زیادی داشت. این شهر تقریباً بزرگترین شهر به زادگاهش بود، در آنجا به زبان آلمانی صحبت میشد و در این مرکز فرهنگی، هنر و موسیقی، و لذتهای زیادی برای دنبال کردن وجود داشت. علاوه بر این، برادر بزرگتر کورت از قبل آنجا بود و در دانشگاه تحصیل میکرد. وقتی کورت به وین رسید با برادرش در آپارتمان کوچکی که فاصله چندانی از دانشگاه نداشت زندگی میکرد. رودولف از برادر کوچکترش که گهگاه از بیماریهای خفیفی که در طول زندگیاش او را آزار میداد، مراقبت میکرد. بخشی از این بیماریها واقعی، و بخشی هم خیالی بودند.
کورت شروع به گذراندن دورههای ریاضیات کرد و تحت تأثیر سخنرانیهای برخی از اساتید مشهور وین قرار گرفت. یکی از آنها هانس هان (Hans Hahn) (1879-1934) ریاضیدان اتریشی بود. هان در سال 1905 دکترای خودش در ریاضیات را از دانشگاه وین گرفت. او در جنگ جهانی اول خدمت کرد و در نبرد به شدت مجروح شد. هان پس از بهبودی به دانشگاه بُن رفت و در آنجا به عنوان استاد تمام ریاضیات منصوب شد. به نظر میرسد که هان دلتنگ وین بود و در تابستان 1921، در حالی که کورت و خانوادهاش در چشمههای مارینباد مشغول تفریح بودند، هان به شهر خود بازگشت و در دانشگاه وین به عنوان استاد مشغول به کار شد. او در بسیاری از زمینهها مشارکت داشت، اما مهمترین کار او در ریاضیات، قضیه معروفِ هان-باناخ بود که به طور مشترک به او و استفان باناخ نسبت داده میشود.

هانس هان (1879-1934)
قضیه هان-باناخ مربوط به آنالیز تابعی (functional analysis) است. این قضیه شرایطی را بیان میکند که تحت آن یک تابعی خطی (نگاشتی از یک فضای برداری به خط حقیقی، که هم خطی و هم همگن است) میتواند به کل فضایی که شرایط کرانداری آن تابع را دارد، تعمیم داده شود. قضیه هان-باناخ در آنالیز ریاضی پیشرفته بسیار مهم است. اثبات این قضیه کیفیت مرموزی دارد، زیرا نیاز به استفاده از نتیجهای به نام لمِ زورن (Zorn's lemma) دارد.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א18
گودل از بازگشت به اروپایی که در آستانه بدترین درگیری تاریخ قرار داشت، خشنود بود و از وقایع شوم اواخر دهه ۱۹۳۰ بیخبر مانده بود. او و آدل در وین در حال برنامهریزی برای ازدواج بودند، ازدواجی که قرار بود پس از الحاق اتریش به آلمان در سال ۱۹۳۸ انجام شود. این نیز نشان دیگری بود از اینکه زندگی آنها چقدر از وقایع اطرافشان کاملاً جدا مانده بود.
گفته میشود گودل پس از بازگشت به وین، این جمله را بر زبان آورد: ” Jetzt, Mengenlehre!“، یعنی ”حالا دیگر نوبت نظریه مجموعهها است!“ ، که نشاندهنده تمایل او برای گذاشتن تمام انرژیاش به کار بر روی مسئله لاینحل بینهایتِ بالفعل کانتور بود. او حتماً میدانست که تمرکزش بر روی این مباحث، کمکم او را دیوانه میکند، اما او نیز مانند کانتور، مثل پروانهای که به سمت آتش کشیده میشود، به سوی نورِ بینهایت کشیده میشد. گودل در آسایشگاه و در حالی که دنیای اطرافش در حال فروپاشی بود، دعوتنامههای سخاوتمندانهای که از آمریکا میرسید، و حالا این دعوتنامهها نه فقط موسسه مطالعات پیشرفته، بلکه سایر دانشگاهها را نیز شامل میشد. ولی او آنها را نادیده میگرفت و خود را غرق در مطالعه فرضیه پیوستار کرد.
تلاشهای گودل برای حل مسائل ریاضی، مشکلات روانیاش را تشدید کرد. او تصور میکرد که به دلیل «هوای بدی» که تنفس میکند، مسموم شده است. این هوا از یخچال آپارتمانی که آن موقع او و آدل در آن زندگی میکردند، و همچنین از سیستم گرمایشی میآمد. آدل نسبت به مشکلات او بیتفاوت بود - با اینکه آدل میدانست سیگارهایش موجب بدتر شدن «هوای» خانه میشود، او در تمام طول زندگیاش سیگار میکشید. در طول سالهای ۱۹۳۷ و ۱۹۳۸، گودل تا حد زیادی ناتوان بود. این زوج با پسانداز خودشان زندگی میکردند، که به سرعت در حال تمام شدن بود. تنها درآمد گودل از درسهایی بود که در مورد نظریه اصل موضوعی مجموعهها در دانشگاه تدریس میکرد.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א19
گودل نیز مانند کانتور نمیتوانست قدرت بینهایت بالفعل را تحمل کند. او برای مدت طولانی از دروننگری شدیدی که مطالعه فرضیه پیوستار به همراه داشت، به سمت جنون سقوط میکرد. او میدانست که وقتی فرضیه پیوستار در سیستمی شامل تمام اصول موضوعه نظریه مجموعهها قرار گیرد، باعث تناقض نمیشود. او همچنین ثابت کرده بود که اصلِ موضوعه انتخاب برای استفاده در این اصول «ایمن» است. اما او نمیدانست که آیا عکس این قضیه نیز صادق است یا خیر. او نمیدانست که آیا نفی فرضیه پیوستار و نفی اصل موضوع انتخاب نیز با نظریه مجموعهها سازگار هستند یا خیر. او ماههای زیادی را با اندوه در فکر فرو رفت و سعی کرد ثابت کند که فرضیه پیوستار کاملاً مستقل از بقیه ریاضیات است. این در صورتی صادق است که نفی فرضیه پیوستار نیز با اصول نظریه مجموعهها سازگار باشد.
گودل تعطیلات تابستانی را در سواحل ایالت مین گذراند. او شبها را با قدم زدن در کنار جنگل ساحلی و تمرکز عمیق سپری میکرد. مردم ساکن اقامتگاه او را به عنوان «آلمانی» میشناختند، و وقتی شبها او را در ساحل تنها میدیدند، برخی فکر میکردند او یک جاسوس است که منتظر ارسال سیگنالهای مخفی به یک زیردریایی است. گودل ارتباطش را با واقعیت نیز از دست میداد. گلکاری اقامتگاه باعث میشد فکر کند در مارینباد است.
گودل هر چه بیشتر به کجخیالی (پارانویا) دچار میشد. او متقاعد شده بود که پزشکانش سعی دارند او را به بیمارستان منتقل کنند. از نظر او، تمام سیستمهای گرمایشی یا تهویه مطبوع گازهای سمی منتشر میکردند، و غذایش مسموم بود. او پرتقال میخواست، اما وقتی به او میدادند، میگفت که خوب نیستند و آنها را پس میفرستاد. او سعی کرد یک اثبات ریاضی برای وجود خدا ابداع کند. او فکر میکرد برای این موضوع اثباتی دارد، سپس به این نتیجه رسید که این اثبات خوب نیست، سپس دوباره آن را قبول میکرد، و بعداً آن را رد میکرد. او هنوز روی مسئله پیوستار کار میکرد، اما سرانجام تمام تلاشها برای حل این مشکل را رها کرد و درگیر مسائل دیگر شد (درست مانند کانتور). در حالی که کانتور سالها بیهوده تلاش کرده بود تا اثبات کند که خودِ شکسپیر نمایشنامههایش را ننوشته، گودل نیز حالا تلاش میکرد تا ثابت کند که لایبنیتس نظریههایی را توسعه بود که احتمالاً کار خود او نیستند. گودل نیز مانند کانتور هیچ اثبات قانعکنندهای برای ادعاهای خود پیدا نکرد. چیزی ماوراءالطبیعه در مورد فرضیه پیوستار وجود داشت، چیزی که تفکر طولانی در مورد آن را غیرممکن میکرد. تلاش برای اثبات آن برای ذهن خطرناک بود؛ چاره این بود که باید آن را رها کرد و به کار دیگری پرداخت.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א20
در بهار ۱۹۶۳، در حالی که گودل ۵۷ ساله درگیر مشکلات سلامتی، و کجپنداریها، و تصوراتش درباره پیوستار و بینهایت بود، و دیگر قادر به تمرکز شدید مورد نیاز چنین کارهای نبود، در آن سوی قاره تحول مهمی در حال وقوع بود.
در دانشگاه استنفورد، ریاضیدان جوانی به نام پل کوهن (Paul Cohen)، از روش جدید و هوشمندانه به نام «اجبار» (forcing) استفاده کرد تا ثابت کند که اصل موضوعه انتخاب مستقل از سایر اصول موضوعه نظریه مجموعهها است و در واقع فرضیه پیوستار مستقل از تمام اصول موضوعه، از جمله اصل موضوع انتخاب، است. کوهن این کار را با اثباتِ مکملِ نتیجهای که سالها قبل توسط خودِ گودل اثبات شده بود، انجام داد. اثبات کوهن به طور قطعی نشان داد که درستی فرضیه پیوستار کانتور را نمیتوان در سیستم فعلی اصول موضوعه نظریه مجموعهها اثبات کرد.
این لزوماً به این معنی نبود که نتیجه ناتمامیت گودل در مورد فرضیه پیوستار صدق کند - هنوز هم ممکن بود سیستم دیگری از اصول موضوعه، اثباتی برای درستی فرضیه پیوستار یا نفی آن را امکانپذیر کند. چیزی که اثبات کوهن به ما گفت این بود که در سیستم فعلی ما از اصول موضوعه، فرضیه پیوستار را میتوان درست یا نادرست در نظر گرفت و هیچ تناقض جدیدی حاصل نمیشود. بنابراین، پس از سالها تلاشِ سخت برای فهمیدن اینکه آیا کانتور درست میگفت یا اشتباه، فرضیه پیوستار همچنان یک معما باقی مانده بود.
برای اثبات درستی فرضیه پیوستار، یا اثبات نادرستی آن (و بنابراین اثبات وجود الفهای دیگر بین الف-صفر و توان پیوستار) به یک سیستم اصل موضوعه متفاوت نیاز است. اما کدام سیستم اصل موضوعه میتواند مورد استفاده قرار گیرد؟ دستگاه زرملو-فرانکل بهترین سیستم موجود بود، سیستمی که به خوبی به ریاضیات خدمت کرده بود؛ منطقدانان چگونه میتوانستند سیستمِ جایگزینی برای آن پیدا کنند؟ هر سیستم دیگری احتمالاً شامل ناسازگاریها یا خطاهایی بود. سیستم زرملو-فرانکل از آزمونِ زمان جان سالم به در برده بود و بسیاری از ویژگیهای مهمِ طرحهای اصل موضوعی را در خود داشت. اما به هیچ وجه نمیتوانست به ما بگوید که آیا فرضیه پیوستار درست است یا خیر.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.
א21
گودل و کوهن ما را به یک درک صریح رساندند: هر چقدر هم که تلاش کنیم، همیشه حقایقی وجود خواهند داشت که برای همیشه فراتر از دسترس ما خواهند بود. انسانها ممکن است هرگز ماهیت عمیقِ بینهایت را درک نکنند. این شاید چیزی باشد که پیروان کابالا در سطح شهودی و بدون نیاز به اثبات ریاضی درک میکردند. بینهایت برای آنها، شامل خدا، یا چیزهایی بود که متعلق به خدا هستند. یکی از این بینهایتها، چالوک (chaluk)، یا ردای درخشانِ نامتناهی خدا بود که هیچ انسانی نمیتوانست به آن نگاه کند.
اما در طول تاریخ فقط تعداد انگشتشماری از افراد یک نگاه کوتاه به بینهایت داشتهاند. درست زمانی که تمدن بشری در حال بیدار شدن بود، ذهنهای تیزبین یونان باستان توانست حقایق انتزاعی شگفتانگیزی را در مورد بینهایت درک کنند - مثلاً پارادوکسهای زنون، و آثار ارشمیدس، اودوکسوس، و دیگران میتوانند گواهی بر این ادعا باشند.
گالیله، پدر فیزیک جدید، در اواخر دوران کاریاش، با حس غریبش در مورد سازوکار جهان، با نگاهی گذرا به یکی از ویژگیهای بینهایتِ گسسته یکی از این افراد بود. بولتزانو، که یک کشیشِ ریاضیدان بود، توانست جهشی به بینهایتِ پیوسته ایجاد کند و ماهیت متناقض مجموعههای بینهایت روی خط حقیقی را درک کند.
اما این فقط گئورگ کانتور، خالق نظریه مجموعهها، بود که حقیقتاً برخی از حقایق مهم در مورد بینهایت را درک کرد و توانست این مفهوم را به سطوح مختلف تقسیم کند. تلاش برای درک معنای واقعی سطوح مختلفِ بینهایت (تلاش برای تشریح بینهایتِ دستنیافتنی و بررسی درونیترین بخشهای آن) ممکن است به قیمت از دست دادن سلامت عقلی او تمام شده باشد. اما کارهای کانتور دری را به سوی بهشت گشود، دری که دیگر هرگز بسته نشد. زیرا پس از کانتور، چه به دلیل خواص بینهایتهایی که او کشف کرده بود، و چه به دلیل پارادوکسها و دامهای وحشتناکی که او و معاصرانش آشکار کرده بودند، دنیای ریاضیات دیگر مانند قبل نبود. با درک بینهایت تا حدودی، و با آشکارتر شدن خطرات ورود بیشتر به تار و پود آن، ریاضیات در قرن گذشته به رشتهای منسجمتر و سازمانیافتهتر تبدیل شده است.
...........................................
محتویات کامل این کتاب در 22 فصل و 230 صفحه منتشر شده، برای ادامه مطالعه این کتاب میتوانید نسخه کامل PDF آن را تهیه کنید.